
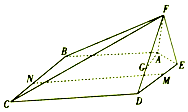
 如图,在五棱锥F-ABCDE中,平面AEF⊥平面ABCDE,AF=EF=1,AB=DE=2,BC=CD=3,且∠AFE=∠ABC=∠BCD=∠CDE=90°.
如图,在五棱锥F-ABCDE中,平面AEF⊥平面ABCDE,AF=EF=1,AB=DE=2,BC=CD=3,且∠AFE=∠ABC=∠BCD=∠CDE=90°.分析 (1)点G为靠近D的三等分点,证明平面AGH∥平面BCF,而AG?平面AGH,可得AG∥平面BCF;
(2)建立空间直角坐标系B-xyz,利用向量方法求直线BM与平面BEF所成角的正弦值.
解答 解:(1)点G为靠近D的三等分点,…(1分)
在线段CD取一点H,使得CH=2,连结AH,GH…(2分)
∵∠ABC=∠BCD=90°,∴AB∥CD.
又AB=CH,∴四边形ABCH为平行四边形,∴AH∥BC,
∵点G为靠近D的三等分点,∴FG:GD=CH:HD=2:1,∴GH∥CF,
∵AH∩GH=H,∴平面AGH∥平面BCF,而AG?平面AGH,∴AG∥平面BCF…(5分)
(2)取AE的中点K,连接FK,∵AF=EF,∴FK⊥AE,又平面AEF⊥平面ABCDE,
∴FK⊥平面ABCDE…(6分)
如图,建立空间直角坐标系B-xyz,则$D({3,3,0}),C({3,0,0}),E({1,3,0}),F({\frac{1}{2},\frac{5}{2},\frac{{\sqrt{2}}}{2}})$.
设EM=m(0<m<2),则M(1+m,3,0)…(7分)
∵翻折后,D与F重合,∴DM=FM,又FM2=KM2+FK2,
故${({m-2})^2}={({m+\frac{1}{2}})^2}+{({\frac{1}{2}})^2}+\frac{1}{2}⇒m=\frac{3}{5}$,从而,$\overrightarrow{BM}$=($\frac{8}{5}$,3,0)…(8分)
$\overrightarrow{BE}$=(1,3,0),$\overrightarrow{BF}$=($\frac{1}{2},\frac{5}{2}$,$\frac{\sqrt{2}}{2}$),
设n=(x,y,z)为平面BEF的一个法向量,
则$\left\{\begin{array}{l}{x+3y=0}\\{\frac{1}{2}x+\frac{5}{2}y+\frac{\sqrt{2}}{2}z=0}\end{array}\right.$,
取x=3,则$n=({3,-1,\sqrt{2}})$…(10分)
设直线BM与平面BEF所成角为α,则sinα=$\frac{\frac{9}{5}}{\frac{17}{5}×2\sqrt{3}}$=$\frac{3\sqrt{3}}{34}$,
故直线BM与平面BEF所成角的正弦值为$\frac{{3\sqrt{3}}}{34}$…(12分)
点评 本题考查平面与平面平行、线面平行的判定,考查向量知识的运用,属于中档题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x2=4,则x=2”的否命题为“若x2=4,则x≠2” | |
| B. | 命题“?x∈R,x2+2x-1<0”的否定是“?x∈R,x2+2x-1>0” | |
| C. | 命题“若x=y,则sinx=siny”的逆否命题为假命题 | |
| D. | 若“p或q”为真命题,则p,q至少有一个为真命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
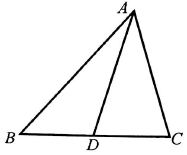 已知a,b,c分别为△ABC三个内角A,B,C的对边,且acosC+$\sqrt{3}$asinC-b-c=0.
已知a,b,c分别为△ABC三个内角A,B,C的对边,且acosC+$\sqrt{3}$asinC-b-c=0.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | {x|1<x<2} | C. | {x|1≤x<2} | D. | {x|1<x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | fs(9)=fT(1) | B. | fs(8)=fT(1) | C. | fs(6)=fT(4) | D. | fs(5)=fT(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com