
 )的围墙,且要求中间用围墙
)的围墙,且要求中间用围墙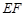 隔开,使得
隔开,使得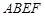 为矩形,
为矩形,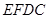 为正方形,设
为正方形,设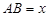 米,已知围墙(包括
米,已知围墙(包括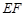 )的修建费用均为800元每米,设围墙(包括
)的修建费用均为800元每米,设围墙(包括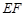 )的修建总费用为
)的修建总费用为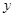 元。
元。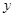 关于
关于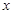 的函数解析式;
的函数解析式;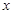 为何值时,设围墙(包括
为何值时,设围墙(包括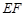 )的的修建总费用
)的的修建总费用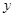 最小?并求出
最小?并求出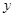 的最小值。
的最小值。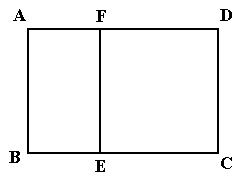
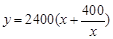
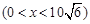 ;(2)当
;(2)当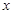 为20米时,
为20米时,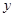 最小.
最小.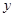 的最小值为96000元.
的最小值为96000元. 米,从而围墙的长度就为:(
米,从而围墙的长度就为:(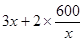 )米,从而修建总费用
)米,从而修建总费用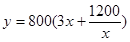 元,只是注意求函数的解析式一定要指出函数的定义域,此题中不仅要
元,只是注意求函数的解析式一定要指出函数的定义域,此题中不仅要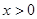 而且还要注意题目中的隐含条件:“中间用围墙
而且还要注意题目中的隐含条件:“中间用围墙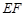 隔开,使得
隔开,使得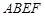 为矩形,
为矩形,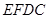 为正方形”从而可知矩形ABCD的长
为正方形”从而可知矩形ABCD的长 应当要大于其宽x,所以x还应满足:
应当要大于其宽x,所以x还应满足: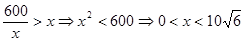 ;(2)由(1)知
;(2)由(1)知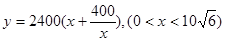 所以可用基本不等式来求y的最小值,及对应的x的值;最后应用问题一定要注意将数学解得的结果还原成实际问题的结果.
所以可用基本不等式来求y的最小值,及对应的x的值;最后应用问题一定要注意将数学解得的结果还原成实际问题的结果.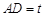 米,则由题意得
米,则由题意得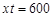 ,且
,且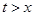 2分
2分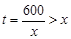 ,可得
,可得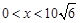 4分
4分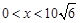 ”扣2分)
”扣2分)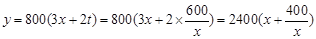 , 6分
, 6分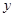 关于
关于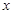 的函数解析式为
的函数解析式为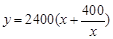
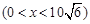 . 7分
. 7分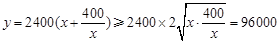 , 10分
, 10分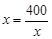 ,即
,即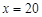 时等号成立. 12分
时等号成立. 12分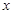 为20米时,
为20米时,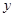 最小.
最小.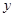 的最小值为96000元. 14分
的最小值为96000元. 14分

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:单选题
| A.所有的素数都不是奇数 | B.有些的素数是奇数 |
| C.存在一个素数不是奇数 | D.存在一个素数是奇数 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 满足2
满足2 +
+ ,对x≠0恒成立,在数列{an}、{bn}中,a1=1,b1=1,对任意x∈N+,
,对x≠0恒成立,在数列{an}、{bn}中,a1=1,b1=1,对任意x∈N+, ,
, 。
。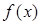 解析式;
解析式; ,总存在自然数k,当n≥k时,
,总存在自然数k,当n≥k时, 恒成立,求k的最小值。
恒成立,求k的最小值。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,
, ,
, 的最小值为
的最小值为 .
. 的解析式;
的解析式; ,若
,若 在
在 上是减函数,求实数
上是减函数,求实数 的取值范围;
的取值范围;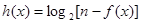 ,若此函数在定义域范围内不存在零点,求实数
,若此函数在定义域范围内不存在零点,求实数 的取值范围.[
的取值范围.[查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com