
【题目】如图,正方体ABCD-A′B′C′D′的棱长为a,连接A′C′,A′D,A′B,BD,BC′,C′D,得到一个三棱锥.求:
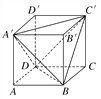
(1)三棱锥A′-BC′D的表面积与正方体表面积的比值;
(2)三棱锥A′-BC′D的体积.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)三棱锥A′BC′D为正四面体,表面积为四个正三角形面积,边长为正方体棱长![]() 倍,根据三角形面积公式以及正方形面积公式求比值(2)三棱锥A′BC′D的体积等于正方体体积减去4个小三棱锥体积.
倍,根据三角形面积公式以及正方形面积公式求比值(2)三棱锥A′BC′D的体积等于正方体体积减去4个小三棱锥体积.
试题解析:(1)∵ABCDA′B′C′D′是正方体,∴六个面都是正方形,∴A′C′=A′B=A′D=BC′=BD=C′D=![]() a,∴S三棱锥=4×
a,∴S三棱锥=4×![]() ×(
×(![]() a)2=2
a)2=2![]() a2,S正方体=6a2,∴
a2,S正方体=6a2,∴![]() =
=![]() .
.
(2)显然,三棱锥A′ABD、C′BCD、DA′D′C′、BA′B′C′是完全一样的,
∴V三棱锥A′BC′D=V正方体-4V三棱锥A′ABD=a3-4×![]() ×
×![]() a2×a=
a2×a=![]() a3.
a3.


科目:高中数学 来源: 题型:
【题目】已知直线l1:(a-1)x+y+b=0,l2:ax+by-4=0,求满足下列条件的a,b的值.
(1)l1⊥l2,且l1过点(1,1);
(2)l1∥l2,且l2在第一象限内与两坐标轴围成的三角形的面积为2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为 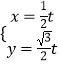 (t为参数),曲线C的参数方程为
(t为参数),曲线C的参数方程为 ![]() (θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为(2
(θ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点P的极坐标为(2 ![]() ,
, ![]() ). (Ⅰ)求直线l以及曲线C的极坐标方程;
). (Ⅰ)求直线l以及曲线C的极坐标方程;
(Ⅱ)设直线l与曲线C交于A,B两点,求△PAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校大一新生中的6名同学打算参加学校组织的“演讲团”、“吉他协会”等五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中没有人参加“演讲团”的不同参加方法数为( )
A.3600
B.1080
C.1440
D.2520
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ax2﹣2lnx,x∈(0,e],其中e是自然对数的底.
(1)若f(x)在x=1处取得极值,求a的值;
(2)求f(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知正方体ABCD-A1B1C1D1.
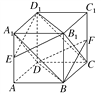
(1)求证:平面A1BD∥平面B1D1C.
(2)若E,F分别是AA1,CC1的中点,求证:平面EB1D1∥平面FBD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:x+2y+1=0,l2:-2x+y+2=0,它们相交于点A.
(1)判断直线l1和l2是否垂直?请给出理由.
(2)求过点A且与直线l3:3x+y+4=0平行的直线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com