
【题目】已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.

(1)求该几何体的体积![]() ;
;
(2)求该几何体的侧面积![]() .
.
科目:高中数学 来源: 题型:
【题目】将圆![]() 每一点的横坐标保持不变,纵坐标变为原来的
每一点的横坐标保持不变,纵坐标变为原来的![]() 倍,得到曲线
倍,得到曲线![]() .
.
(1)写出![]() 的参数方程;
的参数方程;
(2)设直线![]() 与
与![]() 的交点为
的交点为![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,求:过线段
轴的正半轴为极轴建立极坐标系,求:过线段![]() 的中点且与
的中点且与![]() 垂直的直线的极坐标方程.
垂直的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国西部某省4A级风景区内住着一个少数民族村,该村投资了800万元修复和加强民俗文化基础设施,据调查,修复好村民俗文化基础设施后,任何一个月内(每月按30天计算)每天的旅游人数f(x)与第x天近似地满足![]() (千人),且参观民俗文化村的游客人均消费g(x)近似地满足g(x)=143﹣|x﹣22|(元).
(千人),且参观民俗文化村的游客人均消费g(x)近似地满足g(x)=143﹣|x﹣22|(元).
(1)求该村的第x天的旅游收入p(x)(单位千元,1≤x≤30,x∈N*)的函数关系;
(2)若以最低日收入的20%作为每一天的计量依据,并以纯收入的5%的税率收回投资成本,试问该村在两年内能否收回全部投资成本?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率
的离心率![]() ,过点
,过点![]() 和
和![]() 的直线与原点的距离为
的直线与原点的距离为![]() .
.

(1)求椭圆的方程;
(2)设![]() 为椭圆的左、右焦点,过
为椭圆的左、右焦点,过![]() 作直线交椭圆于
作直线交椭圆于![]() 两点,求△
两点,求△![]() 的内切圆半径
的内切圆半径![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,抛物线![]() 的焦点到准线的距离与椭圆
的焦点到准线的距离与椭圆![]() 的长半轴相等,设椭圆的右顶点为
的长半轴相等,设椭圆的右顶点为![]() ,
,![]() 在第一象限的交点为
在第一象限的交点为![]() ,
,![]() 为坐标原点,且
为坐标原点,且![]() 的面积为
的面积为![]() .
.
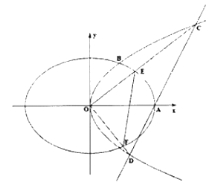
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点.
两点.
①求证:![]() 恒为钝角;
恒为钝角;
②射线![]() 分别交椭圆
分别交椭圆![]() 于
于![]() 两点,记
两点,记![]() 的面积分别是
的面积分别是![]() ,问是否存在直线
,问是否存在直线![]() ,使得
,使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】6月23日15时前后,江苏盐城市阜宁、射阳等地突遭强冰雹、龙卷风双重灾害袭击,风力达12级.灾害发生后,有甲、乙、丙、丁4个轻型救援队从A,B,C,D四个不同的方向前往灾区.已知下面四种说法都是正确的.
(1)甲轻型救援队所在方向不是C方向,也不是D方向;
(2)乙轻型救援队所在方向不是A方向,也不是B方向;
(3)丙轻型救援队所在方向不是A方向,也不是B方向;
(4)丁轻型救援队所在方向不是A方向,也不是D方向;
此外还可确定:如果丙所在方向不是D方向,那么甲所在方向就不是A方向,有下列判断:
①甲所在方向是B方向;②乙所在方向是D方向;③丙所在方向是D方向;④丁所在方向是C方向.
其中判断正确的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com