分析:(I)连接A1C,交AC1于D,连OD则D为A1C的中点,又O为BC的中点,推出A1B∥OD,根据线面平行的判定定理得A1B∥平面AOC1.
(II)连接B1C交OC1于E,连AE,证得OC1⊥B1C,又AO⊥面BCC1B1,得出CAE即为直线AC与平面AOC1所成角,得到所成角之后再在三角形中利用争三角形,求之即可.
解答:解:
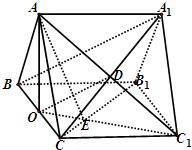
(Ⅰ)连接A
1C,交AC
1于D,连OD
则D为A
1C的中点,
又O为BC的中点
∴A
1B∥OD….….….…(5分)
又A
1B?面AOC
1,OD?面AOC
1∴A
1B∥面AOC
1….….….…(7分)
(II)连接B
1C交OC
1于E,连AE,∵
BC=BB1,∴
==,∴Rt△OCC
1∽Rt△CC
1B
1,
∴∠C
1OC=∠B
1CC
1,∠C
1OC+∠ECO=∠C
1OC+∠B
1CC
1=90°,
∴OC
1⊥B
1C,又AO⊥面BCC
1B
1,
∴AO⊥B
1C,∴B
1C⊥面AOCv,∴∠CAE即为直线AC与平面AOC
1所成角,
又OC=
,CC
1=2,∴OC
1=
,CE=
,
∴sin∠CAE=
==即为所求.
点评:本题是中档题,考查空间几何体的直线与平面所成的角,直线与平面平行的证明,考查空间想象能力,计算能力.

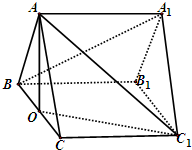 (2011•浙江模拟)已知三棱柱ABC-A1B1C1,底面△ABC为正三角形,AA1⊥平面ABC,BC=
(2011•浙江模拟)已知三棱柱ABC-A1B1C1,底面△ABC为正三角形,AA1⊥平面ABC,BC= (Ⅰ)连接A1C,交AC1于D,连OD
(Ⅰ)连接A1C,交AC1于D,连OD

 阅读快车系列答案
阅读快车系列答案