
分析 令t=ax2-2x+1,则t>0在区间[2,3]上恒成立.再分0<a<1、a>1两种情况,分别根据二次函数的单调性、对数函数的单调性,求得a的范围,综合可得结论.
解答 解:∵函数f(x)=loga(ax2-2x+1)在区间[2,3]是减函数,
令t=ax2-2x+1,则t>0在区间[2,3]上恒成立.
①当0<a<1时,∵f(x)=g(t)=logat,故二次函数t在区间[2,3]上为增函数,
再根据二次函数t的图象的对称轴为x=$\frac{1}{a}$>1,故有$\left\{\begin{array}{l}\frac{1}{a}≤2\\{2}^{2}•a-2×2+1>0\\ 0<a<1\end{array}\right.$,求得$\frac{3}{4}$<a<1;
②当a>1时,根据二次函数t的图象的对称轴为x=$\frac{1}{a}$<1,故二次函数t在区间[2,3]上为增函数,
函数f(x)=loga(ax2-2x+1)在区间[2,3]是增函数,不满足条件.
综上可得,a取值范围为($\frac{3}{4}$,1),
故答案为:($\frac{3}{4}$,1).
点评 本题主要考查对数函数、二次函数的性质,复合函数的单调性,体现了转化的数学思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{1}{6},\frac{1}{2})$ | B. | $(\frac{1}{2},\frac{1}{6})$ | C. | $(\frac{1}{2},-\frac{1}{6})$ | D. | $(\frac{1}{6},-\frac{1}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一个对称中心是(-$\frac{π}{3}$,0) | B. | 一条对称轴方程为x=$\frac{π}{3}$ | ||
| C. | 在区间[-$\frac{π}{3}$,0]上单调递减 | D. | 在区间[0,$\frac{π}{3}$]上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“?x∈R,2x>0”的否定是“?x0∈R,2${\;}^{{x}_{0}}$≤0” | |
| B. | 命题“若xy=0,则x=0或y=0”的否命题为“若xy≠0则x≠0或y≠0” | |
| C. | 若命题p,¬q都是真命题,则命题“p∧q”为真命题 | |
| D. | “x=-1”是“x2-5x-6=0”的必要不充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | S=N,T={-1,1},对应法则是n→(-1)n,n∈S | |
| B. | S={x|x∈R},T={y|y∈R},对应法则是x→y=$\frac{1+x}{1-x}$ | |
| C. | S={0,1,2,5},T={1,$\frac{1}{2}$,$\frac{1}{5}$},对应法则是取倒数 | |
| D. | S={0,1,4,9},T={-3,-2,-1,0,1,2,3},对应法则是开平方. |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
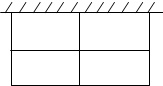 如图,动物园要围成相同面积的长方形虎笼四间,一面可利用原有的墙,其他各面用钢筋网围成.现有可围36m长网的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼的面积最大?
如图,动物园要围成相同面积的长方形虎笼四间,一面可利用原有的墙,其他各面用钢筋网围成.现有可围36m长网的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼的面积最大?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com