
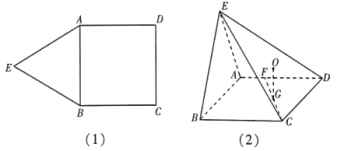
【题目】如图(1),在平面五边形![]() 中,已知四边形
中,已知四边形![]() 为正方形,
为正方形,![]() 为正三角形.沿着
为正三角形.沿着![]() 将四边形
将四边形![]() 折起得到四棱锥
折起得到四棱锥![]() ,使得平面
,使得平面![]() 平面
平面![]() ,设
,设![]() 在线段
在线段![]() 上且满足
上且满足![]() ,
,![]() 在线段
在线段![]() 上且满足
上且满足![]() ,
,![]() 为
为![]() 的重心,如图(2).
的重心,如图(2).
(1)求证:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,连接
,连接![]() ,可知
,可知![]() 三点共线,
三点共线,![]() 三点共线.,因而可得
三点共线.,因而可得![]() 为
为![]() 的重心,再利用线面平行的判定,及可证出;
的重心,再利用线面平行的判定,及可证出;
(2)根据条件,通过面面垂直的性质,证出![]() 平面
平面![]() ,建立空间直角坐标系,标点,求
,建立空间直角坐标系,标点,求![]() 及平面
及平面![]() 的法向量为
的法向量为![]() ,通过利用空间向量法求出线面角.
,通过利用空间向量法求出线面角.
(1)如图,取![]() 的中点
的中点![]() ,
,![]() 的中点
的中点![]() ,连接
,连接![]() .
.
由已知易得![]() 三点共线,
三点共线,![]() 三点共线.
三点共线.
因为![]() ,
,![]() ,所以
,所以![]() .
.
又![]() 为
为![]() 的重心,所以
的重心,所以![]() ,
,
所以![]() .
.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)在![]() 中,因为
中,因为![]() 为
为![]() 的中点,所以
的中点,所以![]() .
.
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
由(1)得,![]() .
.
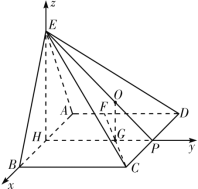
所以![]() 两两垂直,如图,
两两垂直,如图,
分别以射线![]() 的方向为
的方向为![]() 轴的正方向建立空间直角坐标系
轴的正方向建立空间直角坐标系![]() .
.
设![]() ,因为
,因为![]() ,
,![]() ,所以
,所以![]() ,
,
所以![]() ,
,![]() .
.
所以![]() ,
, ,
,![]() ,
,![]() .
.
所以 ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则
所以 令
令![]() ,则
,则![]() ,所以可取
,所以可取![]() .
.
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则
 .
.


科目:高中数学 来源: 题型:
【题目】2018年6月14日,世界杯足球赛在俄罗斯拉开帷幕,世界杯给俄罗斯经济带来了一定的增长,某纪念商品店的销售人员为了统计世界杯足球赛期间商品的销售情况,随机抽查了该商品商店某天200名顾客的消费金额情况,得到如图频率分布表:将消费顾客超过4万卢布的顾客定义为”足球迷”,消费金额不超过4万卢布的顾客定义为“非足球迷”。
消费金额/万卢布 |
|
|
|
|
|
| 合计 |
顾客人数 | 9 | 31 | 36 | 44 | 62 | 18 | 200 |
(1)求这200名顾客消费金额的中位数与平均数(同一组中的消费金额用该组的中点值作代表;
(2)该纪念品商店的销售人员为了进一步了解这200名顾客喜欢纪念品的类型,采用分层抽样的方法从“非足球迷”,“足球迷”中选取5人,再从这5人中随机选取3人进行问卷调查,则选取的3人中“非足球迷”人数的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
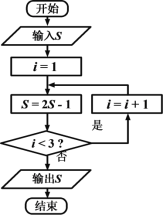
【题目】《算法统宗》是中国古代数学名著,由明代数学家程大位所著,该作完善了珠算口诀,确立了算盘用法,完成了由筹算到珠算的彻底转变,该作中有题为“李白沽酒”“李白街上走,提壶去买酒。遇店加一倍,见花喝一斗,三遇店和花,喝光壶中酒。借问此壶中,原有多少酒?”,如图为该问题的程序框图,若输出的![]() 值为0,则开始输入的
值为0,则开始输入的![]() 值为( )
值为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱ABCD–A1B1C1D1中,已知底面ABCD是菱形,点P是侧棱C1C的中点.
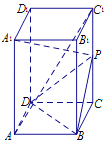
(1)求证:AC1∥平面PBD;
(2)求证:BD⊥A1P.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业要设计制造一批大小、规格相同的长方体封闭水箱,已知每个水箱的表面积为432(每个水箱的进出口所占面积与制作材料的厚度均忽略不计).每个长方体水箱的底面长是宽的2倍.现设每个长方体水箱的底面宽是![]() ,用
,用![]() 表示每个长方体水箱的容积.
表示每个长方体水箱的容积.
(1)试求函数![]() 的解析式及其定义域;
的解析式及其定义域;
(2)当![]() 为何值时,
为何值时,![]() 有最大值,并求出最大值.
有最大值,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一种抛硬币游戏的规则是:抛掷一枚硬币,每次正面向上得1分,反面向上得2分.
(1)设抛掷5次的得分为![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(2)求恰好得到![]() 分的概率.
分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法错误的是( )
A.“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
B.若![]() 为假命题,则
为假命题,则![]() ,
,![]() 均为真命题
均为真命题
C.命题“若![]() ,则
,则![]() ”的逆否命题是“若
”的逆否命题是“若![]() ,则
,则![]() |”
|”
D.若命题![]() ,使得
,使得![]() ,则
,则![]() ,恒有
,恒有![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年非洲猪瘟在东北三省出现,为了进行防控,某地生物医药公司派出技术人员对当地甲乙两个养殖场提供技术服务,方案和收费标准如下:
方案一,公司每天收取养殖场技术服务费40元,对于需要用药的每头猪收取药费2元,不需要用药的不收费;
方案二,公司每天收取养殖场技术服务费120元,若需要用药的猪不超过45头,不另外收费,若需要用药的猪超过45头,超过部分每天收取药费8元.
(1)设日收费为![]() (单位:元),每天需要用药的猪的数量为
(单位:元),每天需要用药的猪的数量为![]() ,试写出两种方案中
,试写出两种方案中![]() 与
与![]() 的函数关系式.
的函数关系式.
(2)若该医药公司从10月1日起对甲养殖场提供技术服务,10月31日该养殖场对其中一个猪舍9月份和10月份猪的发病数量进行了统计,得到如下![]() 列联表.
列联表.
9月份 | 10月份 | 合计 | |
未发病 | 40 | 85 | 125 |
发病 | 65 | 20 | 85 |
合计 | 105 | 105 | 210 |
根据以上列联表,判断是否有![]() 的把握认为猪未发病与医药公司提供技术服务有关.
的把握认为猪未发病与医药公司提供技术服务有关.
附:![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
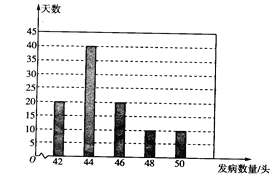
(3)当地的丙养殖场对过去100天猪的发病情况进行了统计,得到如上图所示的条形统计图.依据该统计数据,从节约养殖成本的角度去考虑,若丙养殖场计划结合以往经验从两个方案中选择一个,那么选择哪个方案更合适,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com