
设x,y为实数,满足3≤xy2≤8,4≤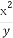 ≤9,则
≤9,则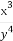 的最大值是 .
的最大值是 .
27
【解析】利用待定系数法,即令 =(
=( )m·(xy2)n,求得m,n后整体代换求解.
)m·(xy2)n,求得m,n后整体代换求解.
设 =(
=( )m(xy2)n,
)m(xy2)n,
则x3y-4=x2m+ny2n-m,
∴ 即
即
∴ =(
=( )2(xy2)-1,
)2(xy2)-1,
又由题意得( )2∈[16,81],
)2∈[16,81],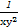 ∈[
∈[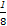 ,
, ],
],
所以 =(
=( )2
)2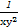 ∈[2,27],
∈[2,27],
故 的最大值是27.
的最大值是27.
【方法技巧】
1.解答本题的关键
设 =(
=( )m(xy2)n是解答本题的关键,体现了待定系数法的思想.本题是幂式之间的关系,与以往的多项式之间的关系相比较是一大创新之处,要注意这一高考新动向.
)m(xy2)n是解答本题的关键,体现了待定系数法的思想.本题是幂式之间的关系,与以往的多项式之间的关系相比较是一大创新之处,要注意这一高考新动向.
2.解决最值问题的新方法
此类问题的一般解法是先用待定系数法把目标式用己知式表示,再利用不等式的性质求出目标式的范围,对于多项式问题,也可以考虑用线性规划的方法求解.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十一第三章第五节练习卷(解析版) 题型:选择题
在△ABC中,tanA+tanB+ =
= tanA·tanB,则C等于( )
tanA·tanB,则C等于( )
(A) (B)
(B) (C)
(C) (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十六第六章第二节练习卷(解析版) 题型:填空题
若关于x的不等式ax2+bx+a2-1≤0的解集分别为[-1,+∞),则实数a,b的值分别为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十八第六章第四节练习卷(解析版) 题型:选择题
已知f(x)=log2(x-2),若实数m,n满足f(m)+f(2n)=3,则m+n的最小值为( )
(A)5 (B)7 (C)8 (D)9
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十八第六章第四节练习卷(解析版) 题型:选择题
设a,b,c∈R,则“abc=1”是“ +
+ +
+ ≤a+b+c”的( )
≤a+b+c”的( )
(A)充分条件但不是必要条件
(B)必要条件但不是充分条件
(C)充分必要条件
(D)既不充分也不必要的条件
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十五第六章第一节练习卷(解析版) 题型:选择题
若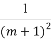 >
>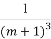 ,则实数m的取值范围是( )
,则实数m的取值范围是( )
(A)m>0 (B)m<-1
(C)-1<m<0 (D)m>0或m<-1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十五第六章第一节练习卷(解析版) 题型:选择题
若a,b是任意实数,且a>b,则 ( )
(A)a2>b2 (B) <1
<1
(C)lg(a-b)>0 (D)( )a<(
)a<( )b
)b
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十二第五章第三节练习卷(解析版) 题型:选择题
等比数列{an}中,若log2(a2a98)=4,则a40a60等于( )
(A)-16(B)10(C)16(D)256
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十七第六章第三节练习卷(解析版) 题型:选择题
若实数x,y满足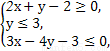 则x2-2xy+y2的取值范围是( )
则x2-2xy+y2的取值范围是( )
(A)[0,4] (B)[0,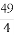 ]
]
(C)[4,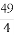 ] (D)[0,
] (D)[0, ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com