
【题目】如图,直角![]() 中,
中,![]() ,
,![]() ,D,E分别是AB,BC边的中点,沿DE将
,D,E分别是AB,BC边的中点,沿DE将![]() 折起至
折起至![]() ,且
,且![]() .
.

(1)求四棱锥![]() 的体积;
的体积;
(2)求证:平面![]() 平面ACF.
平面ACF.
科目:高中数学 来源: 题型:
【题目】已知集合![]() ,集合
,集合![]() ,
,![]() ,
,![]() 满足.
满足.
①每个集合都恰有5个元素
②![]()
![]()
![]()
集合![]() 中元素的最大值与最小值之和称为集合
中元素的最大值与最小值之和称为集合![]() 的特征数,记为
的特征数,记为![]() ,则
,则![]()
![]()
![]() 的值不可能为( )
的值不可能为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某基地蔬菜大棚采用水培、无土栽培方式种植各类蔬菜.过去50周的资料显示,该地周光照量![]() (小时)都在30小时以上,其中不足50小时的周数有5周,不低于50小时且不超过70小时的周数有35周,超过70小时的周数有10周.根据统计,该基地的西红柿增加量
(小时)都在30小时以上,其中不足50小时的周数有5周,不低于50小时且不超过70小时的周数有35周,超过70小时的周数有10周.根据统计,该基地的西红柿增加量![]() (百斤)与使用某种液体肥料
(百斤)与使用某种液体肥料![]() (千克)之间对应数据为如图所示的折线图.
(千克)之间对应数据为如图所示的折线图.

(1)依据数据的折线图,是否可用线性回归模型拟合![]() 与
与![]() 的关系?请计算相关系数
的关系?请计算相关系数![]() 并加以说明(精确到0.01).(若
并加以说明(精确到0.01).(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
(2)蔬菜大棚对光照要求较大,某光照控制仪商家为该基地提供了部分光照控制仪,但每周光照控制仪最多可运行台数受周光照量![]() 限制,并有如下关系:
限制,并有如下关系:
周光照量 |
|
|
|
光照控制仪最多可运行台数 | 3 | 2 | 1 |
若某台光照控制仪运行,则该台光照控制仪周利润为3000元;若某台光照控制仪未运行,则该台光照控制仪周亏损1000元.若商家安装了3台光照控制仪,求商家在过去50周周总利润的平均值.
附:相关系数公式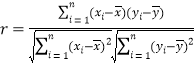 ,参考数据
,参考数据![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代名著《张丘建算经》中记载:“今有方锥,下广二丈,高三丈.欲斩末为方亭,令上方六尺.问:斩高几何?”大致意思是:有一个正四棱锥下底边长为二丈,高三丈,现从上面截去一段,使之成为正四棱台,且正四棱台的上底边长为六尺,则截去的正四棱锥的高是多少.如果我们把求截去的正四棱锥的高改为求剩下的正四棱台的体积,则该正四棱台的体积是(注:1丈![]() 尺)( )
尺)( )
A.1946立方尺B.3892立方尺C.7784立方尺D.11676立方尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某产品的历史收益率的频率分布直方图如图所示.
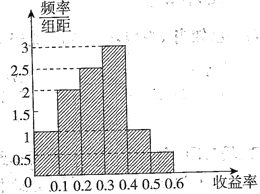
(1)试估计该产品收益率的中位数;
(2)若该产品的售价![]() (元)与销量
(元)与销量![]() (万份)之间有较强线性相关关系,从历史销售记录中抽样得到如表5组
(万份)之间有较强线性相关关系,从历史销售记录中抽样得到如表5组![]() 与
与![]() 的对应数据:
的对应数据:
售价 | 25 | 30 | 38 | 45 | 52 |
销量 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
根据表中数据算出![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,求
,求![]() 的值;
的值;
(3)若从表中五组销量数据中随机抽取两组,记其中销量超过6万份的组数为![]() ,求
,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,
中,![]() 侧面
侧面![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,点E是棱
,点E是棱![]() 的中点.
的中点.

(1)求证:![]() 平面ABC;
平面ABC;
(2)在棱CA上是否存在一点M,使得EM与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作直线
作直线![]() ,交
,交![]() 轴于点
轴于点![]() ,点
,点![]() 满足
满足![]() ,
,![]() 的轨迹为
的轨迹为![]() .
.
(1)求![]() 的方程;
的方程;
(2)已知点![]() ,点
,点![]() ,过
,过![]() 作斜率为
作斜率为![]() 的直线交
的直线交![]() 于
于![]() ,
,![]() 两点,延长
两点,延长![]() ,
,![]() 分别交
分别交![]() 于
于![]() ,
,![]() 两点,记直线
两点,记直线![]() 的斜率为
的斜率为![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
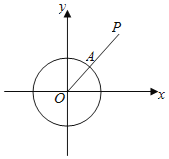
【题目】在平面直角坐标系xOy中,对于⊙O:x2+y2=1来说,P是坐标系内任意一点,点P到⊙O的距离SP的定义如下:若P与O重合,SP=r;若P不与O重合,射线OP与⊙O的交点为A,SP=AP的长度(如图).
(1)直线2x+2y+1=0在圆内部分的点到⊙O的最长距离为_____;
(2)若线段MN上存在点T,使得:
①点T在⊙O内;
②点P∈线段MN,都有ST≥SP成立.则线段MN的最大长度为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com