对于函数f(x)(x∈D),若x∈D时,恒有
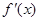
>
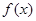
成立,则称函数
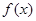
是D上的J函数.
(Ⅰ)当函数f(x)=m
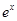
lnx是J函数时,求m的取值范围;
(Ⅱ)若函数g(x)为(0,+∞)上的J函数,
试比较g(a)与
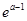
g(1)的大小;
求证:对于任意大于1的实数x
1,x
2,x
3, ,x
n,均有g(ln(x
1+x
2+ +x
n))
>g(lnx
1)+g(lnx
2)+ +g(lnx
n).
(Ⅰ)
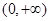
;(Ⅱ)①
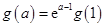
,②先征得
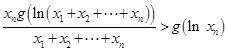
,
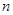
取不同的值得到的式子累加即可得证.
试题分析:(Ⅰ)先求得
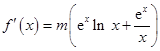
,再由
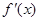
>
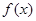
得
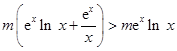
,解得
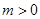
;(Ⅱ)①构造函数
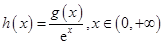
,证明
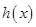
为
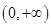
上的增函数,再讨论就可得到
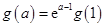
,②先证得
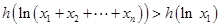
,
即得
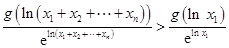
,
整理得
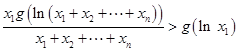
,
同理可得类似的的等式,累加即可得证.
试题解析:(Ⅰ)由
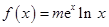
,可得
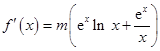
,
因为函数
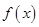
是
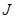
函数,所以
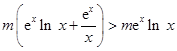
,即
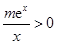
,
因为
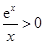
,所以
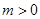
,即
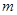
的取值范围为
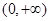
. (3分)
(Ⅱ)①构造函数
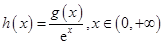
,则
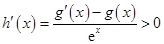
,可得
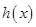
为
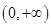
上的增函数,当
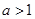
时,
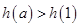
,即
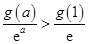
,得
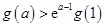
;
当
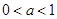
时,
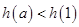
,即
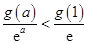
,得
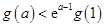
;
当
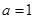
时,
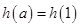
,即
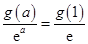
,得
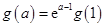
. (6分)
②因为
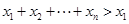
,所以
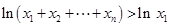
,
由①可知
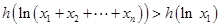
,
所以
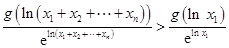
,整理得
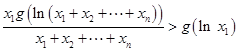
,
同理可得
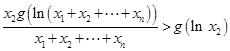
, ,
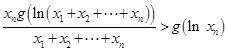
.
把上面
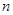
个不等式同向累加可得[
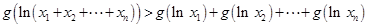
. (12分)
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知函数
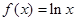
,
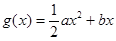
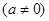
.
(1)若
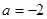
, 函数
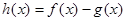
在其定义域是增函数,求
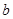
的取值范围;
(2)在(1)的结论下,设函数
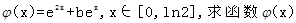
的最小值;
(3)设函数
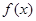
的图象
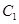
与函数
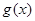
的图象
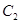
交于点
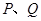
,过线段
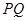
的中点
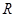
作
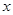
轴的垂线分别交
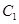
、
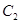
于点
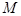
、
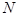
,问是否存在点
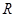
,使
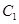
在
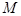
处的切线与
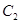
在
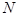
处的切线平行?若存在,求出
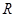
的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
定义域为
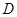
的函数
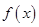
,其导函数为
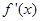
.若对
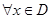
,均有
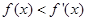
,则称函数
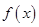
为
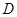
上的梦想函数.
(Ⅰ)已知函数
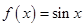
,试判断
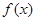
是否为其定义域上的梦想函数,并说明理由;
(Ⅱ)已知函数
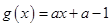
(
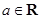
,
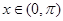
)为其定义域上的梦想函数,求
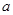
的取值范围;
(Ⅲ)已知函数
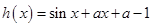
(
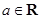
,
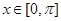
)为其定义域上的梦想函数,求
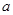
的最大整数值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
下列函数中,既是偶函数又在区间(0,+
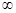
)上单调递减的是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
设实数
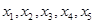
均不小于1,且
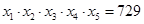
,则
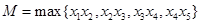
的最小值是
.(
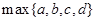
是指
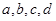
四个数中最大的一个)
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
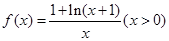
.
(1) 试判断函数
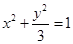
在
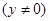
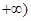
上单调性并证明你的结论;
(2) 若
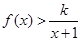
恒成立, 求整数
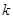
的最大值;
(3) 求证:
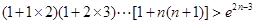
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
f(
x)=ln
x,
g(
x)=
k·
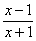
.
(I)求函数F(
x)=
f(
x)-
g(
x)的单调区间;
(Ⅱ)当
x>1时,函数
f(
x)>
g(
x)恒成立,求实数
k的取值范围;
(Ⅲ)设正实数
a1,
a2,
a3,,
an满足
a1+
a2+
a3++
an=1,
求证:ln(1+
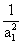
)+ln(1+
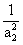
)++ln(1+
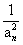
)>
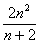
.
查看答案和解析>>

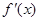 >
>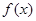 成立,则称函数
成立,则称函数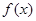 是D上的J函数.
是D上的J函数.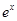 lnx是J函数时,求m的取值范围;
lnx是J函数时,求m的取值范围;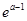 g(1)的大小;
g(1)的大小;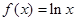 ,
, 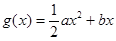
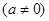 .
.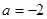 , 函数
, 函数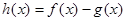 在其定义域是增函数,求
在其定义域是增函数,求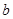 的取值范围;
的取值范围;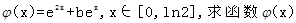 的最小值;
的最小值;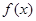 的图象
的图象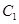 与函数
与函数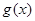 的图象
的图象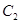 交于点
交于点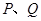 ,过线段
,过线段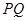 的中点
的中点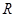 作
作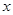 轴的垂线分别交
轴的垂线分别交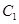 、
、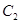 于点
于点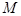 、
、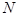 ,问是否存在点
,问是否存在点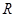 ,使
,使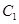 在
在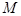 处的切线与
处的切线与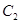 在
在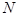 处的切线平行?若存在,求出
处的切线平行?若存在,求出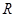 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.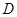 的函数
的函数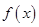 ,其导函数为
,其导函数为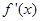 .若对
.若对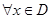 ,均有
,均有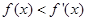 ,则称函数
,则称函数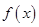 为
为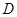 上的梦想函数.
上的梦想函数.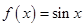 ,试判断
,试判断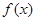 是否为其定义域上的梦想函数,并说明理由;
是否为其定义域上的梦想函数,并说明理由;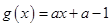 (
(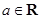 ,
,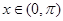 )为其定义域上的梦想函数,求
)为其定义域上的梦想函数,求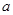 的取值范围;
的取值范围;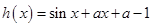 (
(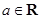 ,
,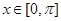 )为其定义域上的梦想函数,求
)为其定义域上的梦想函数,求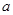 的最大整数值.
的最大整数值.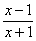 .
.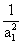 )+ln(1+
)+ln(1+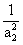 )++ln(1+
)++ln(1+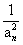 )>
)>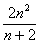 .
.