
【题目】已知圆M:x2+y2+4x﹣2y+3=0,直线l过点P(﹣3,0),圆M的圆心坐标是;若直线l与圆M相切,则切线在y轴上的截距是
【答案】(﹣2,1);﹣3
【解析】解:圆的标准方程为(x+2)2+(y﹣1)2=2, 则圆心坐标为(﹣2,1),半径R= ![]() ,
,
设切线斜率为k,
过P的切线方程为y=k(x+3),
即kx﹣y+3k=0,
则圆心到直线的距离d= ![]() =
= ![]() ,
,
平方得k2+2k+1=(k+1)2=0,
解得k=﹣1,
此时切线方程为y=﹣x﹣3,
即在y轴上的截距为﹣3,
所以答案是:(﹣2,1),﹣3.
【考点精析】本题主要考查了圆的一般方程的相关知识点,需要掌握圆的一般方程的特点:(1)①x2和y2的系数相同,不等于0.②没有xy这样的二次项;(2)圆的一般方程中有三个特定的系数D、E、F,因之只要求出这三个系数,圆的方程就确定了;(3)、与圆的标准方程相比较,它是一种特殊的二元二次方程,代数特征明显,圆的标准方程则指出了圆心坐标与半径大小,几何特征较明显才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】某小区提倡低碳生活,环保出行,在小区提供自行车出租.该小区有40辆自行车供小区住户租赁使用,管理这些自行车的费用是每日92元,根据经验,若每辆自行车的日租金不超过5元,则自行车可以全部出租,若超过5元,则每超过1元,租不出的自行车就增加2辆,为了便于结算,每辆自行车的日租金x元只取整数,用f(x)元表示出租自行车的日纯收入(日纯收入=一日出租自行车的总收入﹣管理费用)
(1)求函数f(x)的解析式及其定义域;
(2)当租金定为多少时,才能使一天的纯收入最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥P﹣ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面 ABCD,且PA=AD=DB= ![]() ,AB=1,M是PB的中点.
,AB=1,M是PB的中点. 
(1)证明:面PAD⊥面PCD;
(2)求AC与PB所成的角;
(3)求平面AMC与平面BMC所成二面角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义运算为:a*b= ![]() ,如1*2=1,则函数f(x)=|2x*2﹣x﹣1|的值域为( )
,如1*2=1,则函数f(x)=|2x*2﹣x﹣1|的值域为( )
A.[0,1]
B.[0,1)
C.[0,+∞)
D.[1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一块地皮![]() ,其中
,其中![]() ,
, ![]() 是直线段,曲线段
是直线段,曲线段![]() 是抛物线的一部分,且点
是抛物线的一部分,且点![]() 是该抛物线的顶点,
是该抛物线的顶点, ![]() 所在的直线是该抛物线的对称轴.经测量,
所在的直线是该抛物线的对称轴.经测量, ![]() km,
km, ![]() km,
km, ![]() .现要从这块地皮中划一个矩形
.现要从这块地皮中划一个矩形![]() 来建造草坪,其中点
来建造草坪,其中点![]() 在曲线段
在曲线段![]() 上,点
上,点![]() ,
, ![]() 在直线段
在直线段![]() 上,点
上,点![]() 在直线段
在直线段![]() 上,设
上,设![]() km,矩形草坪
km,矩形草坪![]() 的面积为
的面积为![]() km2.
km2.
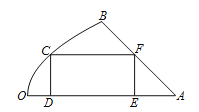
(1)求![]() ,并写出定义域;
,并写出定义域;
(2)当![]() 为多少时,矩形草坪
为多少时,矩形草坪![]() 的面积最大?
的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图甲,已知矩形![]() 中,
中, ![]() 为
为![]() 上一点,且
上一点,且![]() ,垂足为
,垂足为![]() ,现将矩形
,现将矩形![]() 沿对角线
沿对角线![]() 折起,得到如图乙所示的三棱锥
折起,得到如图乙所示的三棱锥![]() .
.

(Ⅰ)在图乙中,若![]() ,求
,求![]() 的长度;
的长度;
(Ⅱ)当二面角![]() 等于
等于![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前项n和为Sn , 且3Sn=4an﹣4.又数列{bn}满足bn=log2a1+log2a2+…+log2an .
(1)求数列{an}、{bn}的通项公式;
(2)若 ![]() ,求使得不等式
,求使得不等式 ![]() 恒成立的实数k的取值范围.
恒成立的实数k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com