
【题目】一个多面体的直观图和三视图如图,M是A1B的中点,N是棱B1C1上的任意一点(含顶点). 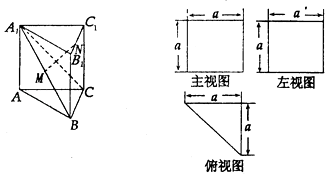
①当点N是棱B1C1的中点时,MN∥平面ACC1A1;
②MN⊥A1C;
③三棱锥N﹣A1BC的体积为VN﹣A ![]() BC=
BC= ![]() a3;
a3;
④点M是该多面体外接球的球心.
其中正确的是 .
【答案】①②③④
【解析】解:①M连接AB中点E,N连接BC中点F,得到MNFE平行于平面ACC1A1 , 面面平行线面平行,①正确;②M连接A1C中点G,连接C1G,A1C⊥平面MNC1G.∴MN⊥A1C;②正确;③三棱锥N﹣A1BC的体积为VN﹣A= ![]() =
= ![]() =
= ![]() a3 , ③正确;④由三视图可知:此多面体是正方体切割下来了的,M是A1B的中点(空间对角线中点),是正方体中心,∴点M是该多面体外接球的球心.故④正确.
a3 , ③正确;④由三视图可知:此多面体是正方体切割下来了的,M是A1B的中点(空间对角线中点),是正方体中心,∴点M是该多面体外接球的球心.故④正确.
所以答案是:①②③④.
【考点精析】掌握棱柱的结构特征是解答本题的根本,需要知道两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形.


 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ),(A>0,ω>0,|φ|< ![]() )的图象与y轴的交点为(
)的图象与y轴的交点为( ![]() ),它在y轴右侧的第一个最高点和最低点分别为(x0 , 3),(x0+2π,﹣3).
),它在y轴右侧的第一个最高点和最低点分别为(x0 , 3),(x0+2π,﹣3).
(1)求函数y=f(x)的解析式;
(2)该函数的图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到?
(3)求这个函数的单调递增区间和对称中心.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分) 已知中心在原点,焦点在![]() 轴上的椭圆C的离心率为
轴上的椭圆C的离心率为![]() ,且经过点
,且经过点![]() .
.
(1)求椭圆C的方程;
(2)是否存在过点![]() 的直线
的直线![]() 与椭圆C相交于不同的两点
与椭圆C相交于不同的两点![]() ,满足
,满足![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是首项为a1= ![]() ,公比q=
,公比q= ![]() 的等比数列,设bn+2=3
的等比数列,设bn+2=3 ![]() an(n∈N*),数列{cn}满足cn=anbn .
an(n∈N*),数列{cn}满足cn=anbn .
(1)求证:{bn}是等差数列;
(2)求数列{cn}的前n项和Sn;
(3)若cn≤ ![]() m2+m﹣1对一切正整数n恒成立,求实数m的取值范围.
m2+m﹣1对一切正整数n恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:x+my+1=0和l2:(m﹣3)x﹣2y+(13﹣7m)=0.
(1)若l1⊥l2 , 求实数m的值;
(2)若l1∥l2 , 求l1与l2之间的距离d.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=8,BC=6,AB=2,E,F分别在BC,AD上,EF∥AB,现将四边形ABEF沿EF折起,使得平面ABEF⊥平面EFDC. 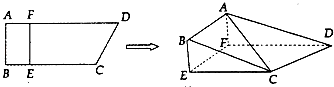
(1)若BE=3,求几何体BEC﹣AFD的体积;
(2)求三棱锥A﹣CDF的体积的最大值,并求此时二面角A﹣CD﹣E的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知中心在原点,焦点在![]() 轴上的椭圆的一个焦点为
轴上的椭圆的一个焦点为![]() ,
, 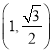 是椭圆上的一个点.
是椭圆上的一个点.
(1)求椭圆的标准方程;
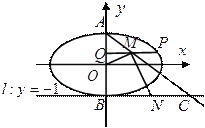
(2)设椭圆的上、下顶点分别为![]() ,
, ![]() (
(![]() )是椭圆上异于
)是椭圆上异于![]() 的任意一点,
的任意一点, ![]() 轴,
轴, ![]() 为垂足,
为垂足, ![]() 为线段
为线段![]() 中点,直线
中点,直线![]() 交直线
交直线![]() 于点
于点![]() ,
, ![]() 为线段
为线段![]() 的中点,如果
的中点,如果![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,M和N分别为BC、C1C的中点,那么异面直线MN与AC所成的角等于( )
A.30°
B.45°
C.60°
D.90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com