
【题目】如图所示,在四棱锥![]() 中,
中,![]() 是正三角形,四边形
是正三角形,四边形![]() 为直角梯形,点
为直角梯形,点![]() 为
为![]() 中点,且
中点,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
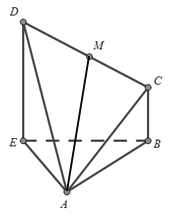
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】将向量![]() =(
=(![]() ,
, ![]() ),
), ![]() =(
=(![]() ,
, ![]() ),…
),…![]() =(
=(![]() ,
,![]() )组成的系列称为向量列{
)组成的系列称为向量列{![]() },并定义向量列{
},并定义向量列{![]() }的前
}的前![]() 项和
项和![]() .如果一个向量列从第二项起,每一项与前一项的差都等于同一个向量,那么称这样的向量列为等差向量列。若向量列{
.如果一个向量列从第二项起,每一项与前一项的差都等于同一个向量,那么称这样的向量列为等差向量列。若向量列{![]() }是等差向量列,那么下述四个向量中,与
}是等差向量列,那么下述四个向量中,与![]() 一定平行的向量是 ( )
一定平行的向量是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某烘焙店加工一个成本为60元的蛋糕,然后以每个120元的价格出售,如果当天卖不完,剩下的这种蛋糕作餐厨垃圾处理.
(1)若烘焙店一天加工16个这种蛋糕,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:个,
(单位:个,![]() )的函数解析式;
)的函数解析式;
(2)为了解该种蛋糕的市场需求情况与性別是否有关,随机统计了100人的购买情况,得如下列联表:
男 | 女 | 合计 | |
购买 | 15 | 35 | 50 |
不购买 | 6 | 44 | 50 |
合计 | 21 | 79 | 100 |
问:能否有![]() 的把握认为是否购买蛋糕与性別有关?
的把握认为是否购买蛋糕与性別有关?
附: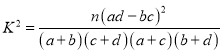
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AD//BC,BC=2AD,AD⊥CD,PD⊥平面ABCD,E为PB的中点.
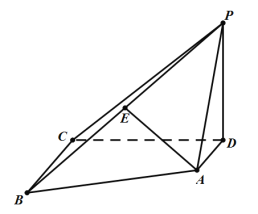
(1)求证:AE//平面PDC;
(2)若BC=CD=PD,求直线AC与平面PBC所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() .
.
(1)根据![]() 不同取值,讨论函数
不同取值,讨论函数![]() 的奇偶性;
的奇偶性;
(2)若![]() ,对于任意的
,对于任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若已知![]() ,
,![]() . 设函数
. 设函数![]() ,
,![]() ,存在
,存在![]() 、
、![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列叙述正确的是( )
A.命题“p且q”为真,则![]() 恰有一个为真命题
恰有一个为真命题
B.命题“已知![]() ,则“
,则“![]() ”是“
”是“![]() ”的充分不必要条件”
”的充分不必要条件”
C.命题![]() 都有
都有![]() ,则
,则![]() ,使得
,使得![]()
D.如果函数![]() 在区间
在区间![]() 上是连续不断的一条曲线,并且有
上是连续不断的一条曲线,并且有![]() ,那么函数
,那么函数![]() 在区间
在区间![]() 内有零点
内有零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆锥的底面半径![]() ,高
,高![]() ,点
,点![]() 是底面直径
是底面直径![]() 所对弧的中点,点
所对弧的中点,点![]() 是母线
是母线![]() 的中点.
的中点.
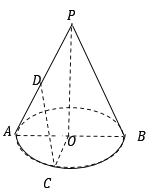
(1)求圆锥的侧面积和体积;
(2)求异面直线![]() 与
与![]() 所成角的大小.(结果用反三角函数表示)
所成角的大小.(结果用反三角函数表示)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三年级有男生220人,学籍编号为1,2,…,220;女生380人,学籍编号为221,222,…,600.为了解学生学习的心理状态,按学籍编号采用系统抽样的方法从这600名学生中抽取10人进行问卷调查(第一组采用简单随机抽样,抽到的号码为10),再从这10名学生中随机抽取3人进行座谈,则这3人中既有男生又有女生的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com