
����Ŀ��ijУΪ�˹���ѧ�����Ĺ��棬������ᣬ�����ˡ������幤�硱.2017��12�£���У�������幤�硱Ϊѧ���ṩ��4�βμӹ����Ļ��ᣬѧ����ͨ����·ƽ̨�����μӻ.Ϊ�˽�ѧ��ʵ�ʲμ���4�λ���������У�����ȡ100��ѧ�����е��飬����ͳ�����±������С��̡���ʾ�μӣ���������ʾδ�μ�.

���Ӹ�У����ѧ������ȡһ�ˣ��Թ�����2017��12��ǡ�μ���2��ѧУ��֯�Ĺ����ĸ��ʣ�
���������ѳ�ȡ��100��ѧ���У�2017��12��ǡ�μ���1�λ��ѧ����4�λ��δ�μӵ�ѧ����17�ˣ���![]() ��ֵ��
��ֵ��
������ѧ���μ�ÿ�ι����ɻ��10��������֣��Թ��Ƹ�У4000��ѧ���У�2017��12�»�õĹ�����ֲ�����30�ֵ�����.
���𰸡�����![]() ����
����![]() (3)1080
(3)1080
�������������������������Ƶ�ʹ��Ƹ��ʽ��м��㼴�ɣ�
����������![]() �����ɵ�
�����ɵ�![]() ��ֵ��
��ֵ��
������![]() ���ɵý�.
���ɵý�.
���������
�⣺�����衰�Ӹ�У����ѧ������ȡһ�ˣ���2017��12��ǡ��2�βμӹ�����Ϊ�¼�![]() ��
��
��![]() .
.
���ԴӸ�У����ѧ������ȡһ�ˣ���2017��12��ǡ��2�βμӹ����ĸ���Ϊ![]() .
.
����������![]() ��
��
����![]() .
.
����![]() .
.
���Թ��Ƹ�У4000��ѧ���У�12�»�õĹ�����ֲ�����30�ֵ�����ԼΪ1080��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Э��Ϊ���˽�õ�������˯ǰ�����ʱ��������Ӹõ���˯ǰ����ľ��������ѡȡ��n�˽��е��飬�ֽ�����������ͳ�Ƶõ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��������˵����ȷ����(����)

A. ˯ǰ����ʱ�����40��50���ӵ�Ƶ��Ϊ0.03
B. ˯ǰ����ʱ�����30���ӵ�Ƶ��Ϊ0.67
C. ��n��1000����ɹ��Ʊ��ε�����˯ǰ����ʱ�����30��50���ӵ���67��
D. ��n��1000����ɹ��Ʊ��ε�����˯ǰ����ʱ�����20��40���ӵ���600��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f(x)Ϊ������R�ϵ�ż��������x��0ʱ����f(x��1)����f(x)���ҵ�x��[0,1)ʱ��f(x)��log2(x��1)��������������
��f(2014)��f(��2015)��0��
������f(x)�ڶ�������������Ϊ2�ĺ�����
��ֱ��y��x�뺯��f(x)��ͼ����2�����㣻
������f(x)��ֵ��Ϊ(��1,1)��
������ȷ����(����)
A. �٢� B. �ڢ�
C. �٢� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �Ľ���ΪF,ֱ��
�Ľ���ΪF,ֱ��![]() ��x��Ľ���ΪP,�������ߵĽ���ΪQ,��
��x��Ľ���ΪP,�������ߵĽ���ΪQ,��![]() .
.
(1)�������ߵķ���;
(2)��F��ֱ��l���������ཻ��A,D����,��Բ![]() �ཻ��B,C����(A,B��������),��A,D����ֱ��������ߵ�����,���������ཻ�ڵ�M,���ABM���CDM�����֮������Сֵ.
�ཻ��B,C����(A,B��������),��A,D����ֱ��������ߵ�����,���������ཻ�ڵ�M,���ABM���CDM�����֮������Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����f(x)�Ƕ�����ΪR�����ں�������С������Ϊ2����
f(1��x)��f(1��x)������1��x��0ʱ��f(x)����x.
(1)�ж�f(x)����ż�ԣ�
(2)���������f(x)������[��1��2]�ϵı���ʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˹���ѧ�����Ĺ��棬������ᣬ�����ˡ������幤�硱.2017��12�£���У�������幤�硱Ϊѧ���ṩ��4�βμӹ����Ļ��ᣬѧ����ͨ����·ƽ̨�����μӻ.Ϊ�˽�ѧ��ʵ�ʲμ���4�λ���������У�����ȡ100��ѧ�����е��飬����ͳ�����±������С��̡���ʾ�μӣ���������ʾδ�μ�.
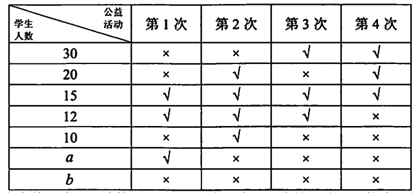
���ݱ������ݹ��ƣ���У4000��ѧ����Լ��120����4�λ��δ�μ�.
������![]() ��ֵ��
��ֵ��
���Ӹ�У4000��ѧ������ȡһ�ˣ��Թ�����2017��12��ǡ�μ���2��ѧУ��֯�Ĺ����ĸ��ʣ�
������֪ѧ��ÿ�βμӹ����ɻ��10��������֣���ȡ��Уһ��ѧ�����Ǹ���2017��12�»�õĹ������Ϊ![]() �����������
�����������![]() �ķֲ��к���ѧ����
�ķֲ��к���ѧ����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ڣ�0��+�ޣ��ϵĵ�������f��x����x�ʣ�0��+�ޣ���f[f��x����lnx]=1����f��x����f�䣨x��=1�Ľ����������� ��������
A. ��2��3�� B. ![]() C.
C. ![]() D. ��1��2��
D. ��1��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ��������![]() �У�
�� ![]() ��
�� ![]() ��
�� ![]() ���ı���
���ı���![]() Ϊ�����Σ�ƽ��
Ϊ�����Σ�ƽ��![]() ƽ��
ƽ��![]() ��
��
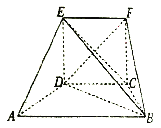
��1��֤�������߶�![]() �ϴ���һ��
�ϴ���һ��![]() ��ʹ��
��ʹ��![]() ƽ��
ƽ��![]() ��
��
��2����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ɫ�������������ij��з�ʽ���ڹ��ڵõ�Ѹ���ƹ�.�����ij������ij��������ɷ���10����ʿ��10��Ůʿ�������ʿ��Ůʿ�зֱ���7�ˡ�6�˱�ʾ�������ﹲ���������С��������˱�ʾ�����ٻ�ѡ���ﹲ������������.
��1������Щ��ʿ��Ůʿ�и���ȡһ�ˣ���������һ�ˡ������ﹲ���������С��ĸ��ʣ�
��2������Щ��ʿ�г�ȡһ�ˣ�Ůʿ�г�ȡ���ˣ����������С������ﹲ���������С�������Ϊ![]() ����
����![]() �ķֲ�������ѧ����.
�ķֲ�������ѧ����.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com