
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 右顶点为
右顶点为![]() 过右焦点且垂直于
过右焦点且垂直于![]() 轴的直线与椭圆相交于
轴的直线与椭圆相交于![]() 两点,所得四边形
两点,所得四边形![]() 为菱形,且其面积为
为菱形,且其面积为![]() .
.
(1)求椭圆的方程;
(2)过左焦点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,试求三角形
两点,试求三角形![]() 面积的最大值.
面积的最大值.
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:
【题目】“斗拱”是中国古代建筑中特有的构件,从最初的承重作用,到明清时期集承重与装饰作用于一体.在立柱顶、额枋和檐檩间或构架间,从枋上加的一层层探出成弓形的承重结构叫拱拱与拱之间垫的方形木块叫斗.如图所示,是“散斗”(又名“三才升”)的三视图(三视图中的单位:分米),现计划用一块长方体的海南黄花梨木料加工成该散斗,则长方体木料的最小体积为( )立方分米.
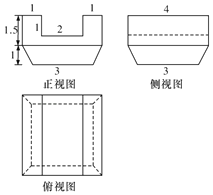
A.40B.![]() C.30D.
C.30D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的中心为坐标原点
的中心为坐标原点![]() 焦点在
焦点在![]() 轴上,右顶点
轴上,右顶点![]() 到右焦点的距离与它到右准线的距离之比为
到右焦点的距离与它到右准线的距离之比为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 是椭圆
是椭圆![]() 上关于
上关于![]() 轴对称的任意两点,设
轴对称的任意两点,设![]() ,连接
,连接![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() .求证:直线
.求证:直线![]() 过定点
过定点![]() 并求出点
并求出点![]() 的坐标;
的坐标;
(3)在(2)的条件下,过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
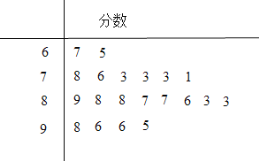
【题目】某大型单位举行了一次全体员工都参加的考试,从中随机抽取了20人的分数.以下茎叶图记录了他们的考试分数(以十位数字为茎,个位数字为叶):若分数不低于95分,则称该员工的成绩为“优秀”.

组别 | 分组 | 频数 | 频率 |
|
1 |
| |||
2 |
| |||
3 |
| |||
4 |
|
(Ⅰ)从这20人中成绩为“优秀”的员工中任取2人,求恰有1人的分数为96的概率;
(Ⅱ)根据这20人的分数补全频率分布表和频率分布直方图,并根据频率分布直方图估计所有员工的平均分数(同一组中的数据用该组区间的中点值作代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,点
,点![]() 在圆内,在过点P所作的圆的所有弦中,弦长最小值为
在圆内,在过点P所作的圆的所有弦中,弦长最小值为![]() .
.
(1)求实数a的值;
(2)若点M为圆外的动点,过点M向圆C所作的两条切线始终互相垂直,求点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着互联网的发展,诸如“滴滴打车”“神州专车”等网约车服务在我国各:城市迅猛发展,为人们出行提供了便利,但也给城市交通管理带来了一些困难.为掌握网约车在![]() 省的发展情况,
省的发展情况,![]() 省某调查机构从该省抽取了
省某调查机构从该省抽取了![]() 个城市,分别收集和分析了网约车的
个城市,分别收集和分析了网约车的![]() 两项指标数
两项指标数![]() ,数据如下表所示:
,数据如下表所示:
城市1 | 城市2 | 城市3 | 城市4 | 城市5 | |
|
|
|
|
|
|
|
|
|
|
|
|
经计算得: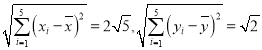
(1)试求![]() 与
与![]() 间的相关系数
间的相关系数![]() ,并利用
,并利用![]() 说明
说明![]() 与
与![]() 是否具有较强的线性相关关系(若
是否具有较强的线性相关关系(若![]() ,则线性相关程度很高,可用线性回归模型拟合);
,则线性相关程度很高,可用线性回归模型拟合);
(2)立![]() 关于
关于![]() 的回归方程,并预测当
的回归方程,并预测当![]() 指标数为
指标数为![]() 时,
时,![]() 指标数的估计值.
指标数的估计值.
附:相关公式: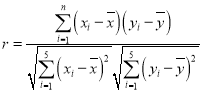 ,
,
参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为正方形,
为正方形,![]() 底面
底面![]() ,
,![]() ,E为线段
,E为线段![]() 的中点.
的中点.
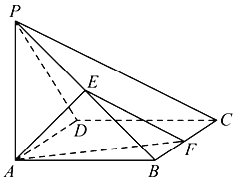
(1)证明:点F在线段![]() 上移动时,
上移动时,![]() 为直角三角形;
为直角三角形;
(2)若F为线段![]() 的中点,求二面角
的中点,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为提高生产效率,需引进一条新的生产线投入生产,现有两条生产线可供选择,生产线①:有A,B两道独立运行的生产工序,且两道工序出现故障的概率依次是0.02,0.03.若两道工序都没有出现故障,则生产成本为15万元;若A工序出现故障,则生产成本增加2万元;若B工序出现故障,则生产成本增加3万元;若A,B两道工序都出现故障,则生产成本增加5万元.生产线②:有a,b两道独立运行的生产工序,且两道工序出现故障的概率依次是0.04,0.01.若两道工序都没有出现故障,则生产成本为14万元;若a工序出现故障,则生产成本增加8万元;若b工序出现故障,则生产成本增加5万元;若a,b两道工序都出现故障,则生产成本增加13万元.
(1)若选择生产线①,求生产成本恰好为18万元的概率;
(2)为最大限度节约生产成本,你会给工厂建议选择哪条生产线?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以
为参数),以![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)曲线![]() 与曲线
与曲线![]() 有两个公共点,求实数
有两个公共点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com