
【题目】如图,在底面是菱形的四棱锥P﹣ABCD中, ![]() E、F分别为PD、AB的中点,△PAB为等腰直角三角形,PA⊥平面ABCD,PA=1.
E、F分别为PD、AB的中点,△PAB为等腰直角三角形,PA⊥平面ABCD,PA=1.

(1)求证:直线AE∥平面PFC;
(2)求证:PB⊥FC.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)取PC的中点M,连接EM,FM.利用三角形中位线定理可得ME平行且等于![]() CD,又AF平行且等于
CD,又AF平行且等于![]() CD,可得AF平行且等于EM,再利用平行四边形的判定与性质定理可得AE∥FM,利用线面平行的判定定理即可证明AE∥平面PFC.(2)由已知利用线面垂直的性质可证PA⊥FC,利用菱形的性质,余弦定理,勾股定理可证CF⊥BF,进而可证CF⊥平面PAB,利用线面垂直的性质可证PB⊥FC.
CD,可得AF平行且等于EM,再利用平行四边形的判定与性质定理可得AE∥FM,利用线面平行的判定定理即可证明AE∥平面PFC.(2)由已知利用线面垂直的性质可证PA⊥FC,利用菱形的性质,余弦定理,勾股定理可证CF⊥BF,进而可证CF⊥平面PAB,利用线面垂直的性质可证PB⊥FC.
试题解析:
(1)取PC的中点M,连接EM,FM.
又E点为PD的中点,∴ME![]()
![]() CD,
CD,
又AF![]()
![]() CD,∴AF
CD,∴AF![]() EM,
EM,
∴四边形AFME是平行四边形,
∴AE∥FM,又AE平面PFC,FM平面PFC,
∴直线AE∥平面PFC.
(2)∵△PAB为等腰直角三角形,PA⊥平面ABCD,PA=1.
∴PA⊥FC,PA⊥AB,PA=AB=1,
∵F为AB的中点,BF=![]() ,
,
∴在底面是菱形的四棱锥P﹣ABCD中,![]() ,可得:BC=1,CF=
,可得:BC=1,CF=![]() ,
,
∴△BFC中,CF2+BF2=BC2,可得:CF⊥BF,
又∵PA∩BA=A,
∴CF⊥平面PAB,
∵PB平面PAB,
∴PB⊥FC.


科目:高中数学 来源: 题型:
【题目】如图,一个直径为1的小圆沿着直径为2的大圆内壁的逆时针方向滚动,M和N是小圆的一条固定直径的两个端点。那么,当小圆这样滚过大圆内壁的一周,点M,N在大圆内所绘出的图形大致是( )

A. 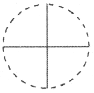 B.
B. 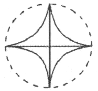 C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线顶点在原点,焦点在![]() 轴上,又知此抛物线上一点
轴上,又知此抛物线上一点![]() 到焦点的距离为6.
到焦点的距离为6.
(1)求此抛物线的方程;
(2)若此抛物线方程与直线![]() 相交于不同的两点
相交于不同的两点![]() 、
、![]() ,且
,且![]() 中点横坐标为2,求
中点横坐标为2,求![]() 的值.
的值.
【答案】(1)![]() ;(2)2.
;(2)2.
【解析】试题分析:
(1)由题意设抛物线方程为![]() ,则准线方程为
,则准线方程为![]() ,解得
,解得![]() ,即可求解抛物线的方程;
,即可求解抛物线的方程;
(2)由![]() 消去
消去![]() 得
得![]() ,根据
,根据![]() ,解得
,解得![]() 且
且![]() ,得到
,得到![]() ,即可求解
,即可求解![]() 的值.
的值.
试题解析:
(1)由题意设抛物线方程为![]() (
(![]() ),其准线方程为
),其准线方程为![]() ,
,
∵![]() 到焦点的距离等于
到焦点的距离等于![]() 到其准线的距离,∴
到其准线的距离,∴![]() ,∴
,∴![]() ,
,
∴此抛物线的方程为![]() .
.
(2)由![]() 消去
消去![]() 得
得![]() ,
,
∵直线![]() 与抛物线相交于不同两点
与抛物线相交于不同两点![]() 、
、![]() ,则有
,则有![]()
解得![]() 且
且![]() ,
,
由![]() ,解得
,解得![]() 或
或![]() (舍去).
(舍去).
∴所求![]() 的值为2.
的值为2.
【题型】解答题
【结束】
20
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形, ![]() ,侧面
,侧面![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上.
上.

(1)求证: ![]() 平面
平面![]() ;
;
(2)如果三棱锥![]() 的体积为
的体积为![]() ,求点
,求点![]() 到面
到面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=aln(x2+1)+bx存在两个极值点x1 , x2 .
(1)求证:|x1+x2|>2;
(2)若实数λ满足等式f(x1)+f(x2)+a+λb=0,试求λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内两点A(4,0),B(0,2)
(1)求过P(2,3)点且与直线AB平行的直线l的方程;
(2)设O(0,0),求△OAB外接圆方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆的两个焦点分别为![]() ,
, ![]() ,过
,过![]() 作椭圆长轴的垂线交椭圆于点
作椭圆长轴的垂线交椭圆于点![]() ,若
,若![]() 为等腰直角三角形,则椭圆的离心率是( )
为等腰直角三角形,则椭圆的离心率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】试题分析:解:设点P在x轴上方,坐标为(![]() ),∵
),∵![]() 为等腰直角三角形,∴|PF2|=|F1F2|,
为等腰直角三角形,∴|PF2|=|F1F2|, ![]() ,故选D.
,故选D.
考点:椭圆的简单性质
点评:本题主要考查了椭圆的简单性质.椭圆的离心率是高考中选择填空题常考的题目.应熟练掌握圆锥曲线中a,b,c和e的关系
【题型】单选题
【结束】
8
【题目】“![]() ”是“对任意的正数
”是“对任意的正数![]() ,
, ![]() ”的( )
”的( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
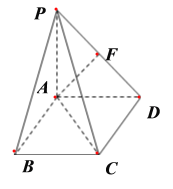
【题目】如图,四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是边长为2的正方形,
PA=AD,F为PD的中点.
(1)求证:AF⊥平面PDC;
(2)求直线AC与平面PCD所成角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com