
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,
的正方形, ![]() 为等边三角形,
为等边三角形, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() 的中点,
的中点, ![]() .
.
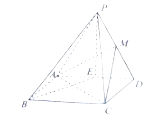
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() .
.
【解析】试题分析:(Ⅰ)根据正三角形的性质可得![]() ,由勾股定理可得
,由勾股定理可得![]() ,由线面垂直的判定定理可得
,由线面垂直的判定定理可得![]() 平面
平面![]() ,从而根据面面垂直的判定定理可得平面
,从而根据面面垂直的判定定理可得平面![]() 平面
平面![]() ;(Ⅱ)根据
;(Ⅱ)根据![]() 平面
平面![]() ,可得
,可得![]() ,结合
,结合![]() ,可得
,可得![]() 平面
平面![]() ,故
,故![]() 为三棱锥
为三棱锥![]() 的高,根据平面几何知识分别算出
的高,根据平面几何知识分别算出![]() 与
与![]() 的面积,由
的面积,由![]() 得,
得, ![]()
![]() 可得点
可得点![]() 到平面
到平面![]() 的距离.
的距离.
试题解析:(Ⅰ)由题意知,正![]() 的边长为
的边长为![]() ,
, ![]() 点
点![]() 为
为![]() 的中点,.
的中点,.
![]() ,
, ![]() .
.
在正方形![]() 中,
中, ![]() 为
为![]() 的中点,边长为
的中点,边长为![]() ,则
,则![]() .
.
在![]() 中,
中, ![]() ,
, ![]() .
.
又![]() ,
, ![]()
![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
![]() 平面
平面![]() ;
;

(Ⅱ)由题意得, ![]() ,
, ![]() 为等边三角形,则
为等边三角形,则![]() ,
, ![]() .
.
![]()
![]() 平面
平面![]() ,
, ![]() .
.
![]() ,
, ![]() 平面
平面![]() .
.
故![]() 为三棱锥
为三棱锥![]() 的高.
的高.
![]()
![]() .
.
又![]()
![]() 是
是![]() 的中点,
的中点, ![]() .
.
在正方形![]() 中,
中, ![]() ,则在
,则在![]() 中,满足
中,满足![]() ,
, ![]() 为直角三角形,
为直角三角形, ![]() .
.
![]() .
.
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,由
,由![]() 得,
得, ![]()
![]() ,解得
,解得![]() .
.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
【题目】已知曲线![]() 是极坐标方程式
是极坐标方程式![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 是参数方程是
是参数方程是 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)设点![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的图像与
的图像与![]() 轴相交于点
轴相交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴相交于点
轴相交于点![]() ,连接
,连接![]() 、
、![]() .
.
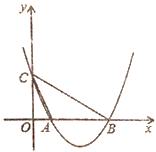
(1)求线段![]() 的长;
的长;
(2)若![]() 平分
平分![]() ,求
,求![]() 的值;
的值;
(3)该函数图象的对称轴上是否存在点![]() ,使得
,使得![]() 为等边三角形?若存在,求出
为等边三角形?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“干支纪年法”是中国历法上自古以来使用的纪年方法,甲、乙、丙、丁、戊、己、庚、辛、壬、癸被称为“十天干”,子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥叫做“十二地支”。“天干”以“甲”字开始,“地支”以“子”字开始,两者按干支顺序相配,组成了干支纪年法,其相配顺序为:甲子、乙丑、丙寅…癸酉,甲戌、乙亥、丙子…癸末,甲申、乙酉、丙戌…癸巳,…,共得到![]() 个组成,周而复始,循环记录。2014年是“干支纪年法”中的甲午年,那么2020年是“干支纪年法”中的()
个组成,周而复始,循环记录。2014年是“干支纪年法”中的甲午年,那么2020年是“干支纪年法”中的()
A. 己亥年 B. 戊戌年 C. 辛丑年 D. 庚子年
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,学校升旗仪式上,主持人站在主席台前沿D处,测得旗杆AB顶部的仰角为![]() 俯角最后一排学生C的俯角为
俯角最后一排学生C的俯角为![]() 最后一排学生C测得旗杆顶部的仰角为
最后一排学生C测得旗杆顶部的仰角为![]() 旗杆底部与学生在一个水平面上,并且不计学生身高.
旗杆底部与学生在一个水平面上,并且不计学生身高.
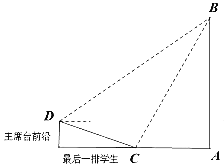
(1)设![]() 米,试用
米,试用![]() 和
和![]() 表示旗杆的高度AB(米);
表示旗杆的高度AB(米);
(2)测得![]() 米,
米,![]() 若国歌长度约为50秒,国旗班升旗手应以多大的速度匀速升旗才能是国旗到达旗杆顶点时师生的目光刚好停留在B处?
若国歌长度约为50秒,国旗班升旗手应以多大的速度匀速升旗才能是国旗到达旗杆顶点时师生的目光刚好停留在B处?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两圆![]() 的圆心分别为
的圆心分别为![]() ,P为一个动点,且直线
,P为一个动点,且直线![]() 的斜率之积为
的斜率之积为![]() .
.
(Ⅰ)求动点P的轨迹M的方程;
(Ⅱ)是否存在过点A(2,0)的直线l与轨迹M交于不同的两点C、D,使得![]() ?若存在,求直线l的方程;若不存在,请说明理由.
?若存在,求直线l的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将正方形![]() 沿对角线
沿对角线![]() 折成直二面角
折成直二面角![]() ,有如下四个结论:
,有如下四个结论:
①![]() ;
;
②![]() 是等边三角形;
是等边三角形;
③![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ;
;
④![]() 与
与![]() 所成的角为
所成的角为![]() .
.
其中错误的结论是____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com