
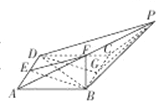
【题目】如图,在四棱锥![]() 中,
中,![]() 是边长为
是边长为![]() 的棱形,且
的棱形,且![]() 分别是
分别是![]() 的中点.
的中点.
(1)证明:![]() 平面
平面![]() ;
;
(2)若二面角![]() 的大小为
的大小为![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.

【答案】(1)见解析(2)![]()
【解析】试题分析:(1)取![]() 中点
中点![]() ,先证明
,先证明![]() 平面
平面![]() ,再证明平面
,再证明平面![]() 平面
平面![]() ,又
,又![]() ,则可得
,则可得![]() 平面
平面![]() (2)先找出
(2)先找出![]() 为二面角
为二面角![]() 的平面角,即
的平面角,即![]() ,接下来证明
,接下来证明![]() 平面
平面![]() ,所以三棱锥
,所以三棱锥![]() 的高为2.再求
的高为2.再求![]() 的面积
的面积![]() ,利用三棱锥
,利用三棱锥![]() 的体积与三棱锥
的体积与三棱锥![]() 的体积相等,即求得点
的体积相等,即求得点![]() 到平面
到平面![]() 的距离.
的距离.
试题解析:
(1)证明:取![]() 中点
中点![]() ,连接
,连接![]() .
.
在![]() 中,
中,![]() ,
,![]() ,所以
,所以![]() 为正角形.
为正角形.
又![]() 为
为![]() 中点,
中点,![]() .
.
因为![]() ,所以
,所以![]() .
.
又![]() ,故
,故![]() 平面
平面![]() .
.
因为![]() 分别是
分别是![]() 的中点,所以
的中点,所以![]() .
.
又![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
又![]() ,故
,故![]() 平面
平面![]() .
.
(2)解:因为![]() 平面
平面![]() ,所以
,所以![]() ,
,![]() ,
,
则![]() 为二面角
为二面角![]() 的平面角,即
的平面角,即![]() .
.
因为![]() ,所以
,所以![]() .
.
因为![]() ,且
,且![]() ,所以
,所以![]() .
.
所以![]() ,且
,且![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
所以![]() 平面
平面![]() ,所以三棱锥
,所以三棱锥![]() 的高为2.
的高为2.
于是三棱锥![]() 的体积
的体积![]() .
.
在![]() 中,
中,![]() ,所以
,所以![]() ,
,![]() .
.
则在![]() 中,
中,
![]() ,
,![]() ,
,![]()
![]()
![]() ,
,
所以![]() ,于是
,于是![]() 的面积
的面积![]() .
.
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,三棱锥
,三棱锥![]() 的体积与三棱锥
的体积与三棱锥![]() 的体积相等,所以
的体积相等,所以![]() ,故
,故![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】【2015高考湖北】如图,圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.
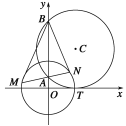
(1)圆C的标准方程为________.
(2)过点A任作一条直线与圆O:x2+y2=1相交于M,N两点,下列三个结论:
①![]() =
=![]() ;②
;②![]() -
-![]() =2;
=2;
③![]() +
+![]() =2
=2![]() .
.
其中正确结论的序号是________(写出所有正确结论的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为评选“全国卫生城市”,从200名志愿者中随机抽取40名志愿者参加街道卫生监督活动,经过统计这些志愿者的年龄介于25岁和55岁之间,为方便安排任务,将所有志愿者按年龄从小到大分成六组,依次为![]() ,如图是按照上述分组方法得到的频率分布直方图的一部分,已知第四组
,如图是按照上述分组方法得到的频率分布直方图的一部分,已知第四组![]() 的人数为4人.
的人数为4人.
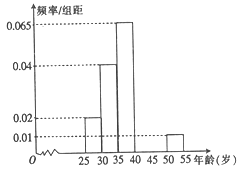
(1)求第五组的频率并估计200名志愿者中年龄在40岁以上(含40岁)的人数;
(2)若从年龄位于第四组和第六组的志愿者中随机抽取两名,记他们的年龄分别为![]() ,事件
,事件![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
, ![]() (
(![]() ).
).
(Ⅰ)求函数![]() 的单调增区间;
的单调增区间;
(Ⅱ)当![]() 时,记
时,记![]() ,是否存在整数
,是否存在整数![]() ,使得关于
,使得关于![]() 的不等式
的不等式![]() 有解?若存在,请求出
有解?若存在,请求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式x2≤5x﹣4的解集为A.
(1)求集合A;
(2)设关于x的不等式x2﹣(a+2)x+2a≤0的解集为M,若MA,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() ,与
,与![]() 轴不重合的直线
轴不重合的直线![]() 经过左焦点
经过左焦点![]() ,且与椭圆
,且与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点,弦
两点,弦![]() 的中点为
的中点为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)若直线![]() 的斜率为1,求直线
的斜率为1,求直线![]() 的斜率;
的斜率;
(Ⅱ)是否存在直线![]() ,使得
,使得![]() 成立?若存在,求出直线
成立?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com