
 在△ABC中,∠A=2∠B,∠C的平分线交AB于点D,∠A的平分线交CD于点E.求证:AD•BC=BD•AC.
在△ABC中,∠A=2∠B,∠C的平分线交AB于点D,∠A的平分线交CD于点E.求证:AD•BC=BD•AC. 分析 证明△ACD~△BCD,所以$\frac{AE}{BD}=\frac{AC}{BC}$,即AE•BC=BD•AC,证明AD=AE,即可证明结论.
解答 证明:因为∠CAB=2∠B,AE为∠CAB的平分线,所以∠CAE=∠B,
又因为CD是∠C的平分线,所以∠ECA=∠DCB,
所以△ACD~△BCD,所以$\frac{AE}{BD}=\frac{AC}{BC}$,即AE•BC=BD•AC,
又因为∠AED=∠CAE+∠ECA,∠ADE=∠B+∠DCB,
所以∠AED=∠ADE,所以AD=AE,
所以AD•BC=BD•AC.
点评 本题主要考查与圆有关的比例线段和相似三角形的判定,证明乘积式的问题可转化证明比例式,最终转化为证明两个三角形相似得到.


科目:高中数学 来源: 题型:选择题
| A. | $C_n^k$ | B. | $C_n^k$2n-k5k | ||
| C. | $C_n^{k-1}$ | D. | $C_n^{k-1}$2n+1-k5k-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,三棱柱ADE-BCF中,四边形ABCD为平行四边形,DE⊥平面ABCD,AD=DE=1,AB=2,∠BCD=60°.
如图,三棱柱ADE-BCF中,四边形ABCD为平行四边形,DE⊥平面ABCD,AD=DE=1,AB=2,∠BCD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | lg(m-n)>0 | B. | ($\frac{1}{2}$)m<($\frac{1}{2}$)n | C. | $\frac{n}{m}$<1 | D. | m2>n2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
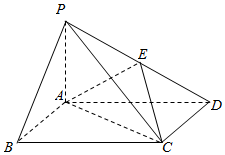 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,且AC=BD,平面PA⊥平面ABCD,E为PD的中点.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,且AC=BD,平面PA⊥平面ABCD,E为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com