
【题目】给出下列四个命题:
①函数![]() 的最小值是2;
的最小值是2;
②等差数列![]() 的前n项和为
的前n项和为![]() ,满足
,满足![]() ,
,![]() ,则当
,则当![]() 时,
时,![]() 取最大值;
取最大值;
③等比数列![]() 的前n项和为
的前n项和为![]() ,若
,若![]() ,
,![]() ,则
,则![]() ;
;
④![]() ,
,![]() 恒成立,则实数a的取值范围是
恒成立,则实数a的取值范围是![]() .
.
其中所有正确命题的序号是________________________.
科目:高中数学 来源: 题型:
【题目】铁人中学高二学年某学生对其亲属30人![]() 饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
饮食习惯进行了一次调查,并用如图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主.)
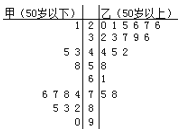
(Ⅰ)根据茎叶图,帮助这位学生说明其亲属30人的饮食习惯;
(Ⅱ)根据以上数据完成下列![]() 的列联表:
的列联表:
主食蔬菜 | 主食肉类 | 合计 | |
50岁以下人数 | |||
50岁以上人数 | |||
合计人数 |
(Ⅲ)能否在犯错误的概率不超过0.01的前提下认为其亲属的饮食习惯与年龄有关系?
附:![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面有五个命题:
①终边在y轴上的角的集合是{β|β=![]() }
}
②设一扇形的弧长为4cm,面积为4cm2,则这个扇形的圆心角的弧度数是2
③![]() 时,
时,![]()
④函数y=x2的图像与函数y=|lgx|的图像的交点个数为2个
所有正确命题的序号是______. (把你认为正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,点
,点![]() 为椭圆
为椭圆![]() 上的动点,若
上的动点,若![]() 的最大值和最小值分别为
的最大值和最小值分别为![]() 和
和![]() .
.
(I)求椭圆![]() 的方程
的方程
(Ⅱ)设不过原点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,若直线
两点,若直线![]() 的斜率依次成等比数列,求
的斜率依次成等比数列,求![]() 面积的最大值
面积的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,椭圆
中,椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上且
上且![]() 轴,直线
轴,直线![]() 交
交![]() 轴于
轴于![]() 点,
点, ![]() ,
, ![]() 为椭圆
为椭圆![]() 的上顶点,
的上顶点, ![]() 的面积为1.
的面积为1.
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() ,且满足
,且满足![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一家水果店的店长为了解本店苹果的日销售情况,记录了过去30天苹果的日销售量(单位:kg),结果如下:
83,96,107,91,70,75,94,80,80,100,
75,99,117,89,74,94,84,85,101,87.
93,85,107,99,55,97,86,84,85,104
(1)请计算该水果店过去30天苹果日销售量的中位数、平均数、极差和标准差
(2)一次进货太多,水果会变得不新鲜;进货太少,又不能满足顾客的需求,店长希望每天的苹果尽量新鲜,又能80%地满足顾客的需求(在100天中,大约有80天可以满足顾客的需求),请问,每天应该进多少千克苹果?
查看答案和解析>>
科目:高中数学 来源: 题型:
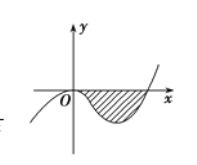
【题目】已知函数![]() 的图象如图,直线
的图象如图,直线![]() 在原点处与函数图象相切,且此切线与函数图象所围成的区域(阴影)面积为
在原点处与函数图象相切,且此切线与函数图象所围成的区域(阴影)面积为![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若常数![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的最大值.
上的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com