
分析 利用条件,求出M的坐标,代入双曲线方程,即可求出双曲线C的渐近线方程.
解答 解:设M(n,m),则$\left\{\begin{array}{l}{\frac{m}{n-b}=2\sqrt{2}}\\{{m}^{2}+(n-b)^{2}=4{b}^{2}}\end{array}\right.$,
∴m=$\frac{4\sqrt{2}}{3}$b,n=$\frac{5}{3}b$,
M代入双曲线方程可得$\frac{\frac{25}{9}{b}^{2}}{{a}^{2}}-\frac{32}{9}=1$,∴$\frac{b}{a}$=$\frac{\sqrt{41}}{5}$,
∴双曲线C的渐近线方程为y=±$\frac{\sqrt{41}}{5}$x,
故答案为y=±$\frac{\sqrt{41}}{5}$x.
点评 本题考查双曲线C的渐近线方程,考查方程思想,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{20}-\frac{y^2}{5}=1$ | B. | $\frac{x^2}{20}-\frac{y^2}{100}=1$ | C. | $\frac{x^2}{5}-\frac{y^2}{20}=1$ | D. | $\frac{x^2}{25}-\frac{y^2}{100}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示为棱长为1的正方体的表面展开图,在原正方体中,给出下列四个结论:
如图所示为棱长为1的正方体的表面展开图,在原正方体中,给出下列四个结论:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 患慢性气管炎 | 未患慢性气管炎 | 合计 | |
| 吸烟 | 20 | 20 | 40 |
| 不吸烟 | 5 | 55 | 60 |
| 合计 | 25 | 75 | 100 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
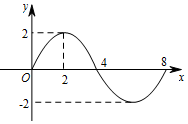 函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象如示,则f(1)+f(2)+f(3)+…+f(210)的值等于( )
函数y=Asin(ωx+φ)(A>0,ω>0)的部分图象如示,则f(1)+f(2)+f(3)+…+f(210)的值等于( )| A. | $\sqrt{2}$ | B. | $2+2\sqrt{2}$ | C. | $2+\sqrt{2}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-4,+∞) | B. | [-4,+∞) | C. | (-3,+∞) | D. | [-3,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com