
【题目】设(1-x)n=a0+a1x+a2x2+…+anxn,n∈N*,n≥2.
(1)设n=11,求|a6|+|a7|+|a8|+|a9|+|a10|+|a11|的值;
(2)设![]() ,Sm=b0+b1+b2+…+bm(m∈N,m≤n-1),求
,Sm=b0+b1+b2+…+bm(m∈N,m≤n-1),求![]() |的值.
|的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)由二项式定理可得ak=(﹣1)k![]() ,再由二项式系数的性质,可得所求和为210;
,再由二项式系数的性质,可得所求和为210;
(2)由组合数的阶乘公式可得bk=(﹣1)k+1![]() ,再由组合数的性质,可得当1≤k≤n﹣1时,bk=(﹣1)k+1
,再由组合数的性质,可得当1≤k≤n﹣1时,bk=(﹣1)k+1![]() (﹣1)k+1(
(﹣1)k+1(![]() )=(﹣1)k﹣1
)=(﹣1)k﹣1![]() (﹣1)k
(﹣1)k![]() ,讨论m=0和1≤m≤n﹣1时,计算化简即可得到所求值.
,讨论m=0和1≤m≤n﹣1时,计算化简即可得到所求值.
(1)由二项式定理可得ak=(﹣1)k![]() ,
,
当n=11时,|a6|+|a7|+|a8|+|a9|+|a10|+|a11|![]()
![]() (
(![]() )=210=1024;
)=210=1024;
(2)bk![]() ak+1=(﹣1)k+1
ak+1=(﹣1)k+1![]() (﹣1)k+1
(﹣1)k+1![]() ,
,
当1≤k≤n﹣1时,bk=(﹣1)k+1![]() (﹣1)k+1(
(﹣1)k+1(![]() )
)
=(﹣1)k+1![]() (﹣1)k+1
(﹣1)k+1![]() (﹣1)k﹣1
(﹣1)k﹣1![]() (﹣1)k
(﹣1)k![]() ,
,
当m=0时,|![]() |=|
|=|![]() |=1;
|=1;
当1≤m≤n﹣1时,Sm=b0+b1+b2+…+bm=﹣1![]() [(﹣1)k﹣1
[(﹣1)k﹣1![]() (﹣1)k
(﹣1)k![]() ]
]
=﹣1+1﹣(﹣1)m![]() (﹣1)m
(﹣1)m![]() ,
,
即有|![]() |=1.
|=1.
综上可得,|![]() |=1.
|=1.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为F1(-c,0),F2(c,0),直线
的左、右焦点分别为F1(-c,0),F2(c,0),直线![]() 交椭圆E于A,B两点,△ABF1的周长为16,△AF1F2的周长为12.
交椭圆E于A,B两点,△ABF1的周长为16,△AF1F2的周长为12.
(1)求椭圆E的标准方程与离心率;
(2)若直线l与椭圆E交于C,D两点,且P(2,2)是线段CD的中点,求直线l的一般方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海轮以每小时30海里的速度航行,在点![]() 测得海面上油井
测得海面上油井![]() 在南偏东
在南偏东![]() ,海轮向北航行40分钟后到达点
,海轮向北航行40分钟后到达点![]() ,测得油井
,测得油井![]() 在南偏东
在南偏东![]() ,海轮改为北偏东
,海轮改为北偏东![]() 的航向再行驶80分钟到达点
的航向再行驶80分钟到达点![]() ,则
,则![]() 两点的距离为(单位:海里)
两点的距离为(单位:海里)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某观测站![]() 在目标
在目标![]() 的南偏西
的南偏西![]() 方向,从
方向,从![]() 出发有一条南偏东
出发有一条南偏东![]() 走向的公路,在
走向的公路,在![]() 处测得与
处测得与![]() 相距
相距![]() 的公路
的公路![]() 处有一个人正沿着此公路向
处有一个人正沿着此公路向![]() 走去,走
走去,走![]() 到达
到达![]() ,此时测得
,此时测得![]() 距离为
距离为![]() ,若此人必须在
,若此人必须在![]() 分钟内从
分钟内从![]() 处到达
处到达![]() 处,则此人的最小速度为( )
处,则此人的最小速度为( )
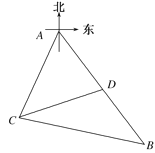
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,![]() 底面ABC,
底面ABC,![]() .点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,
.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,![]() ,
,![]() .
.
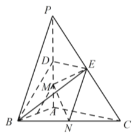
(1)求证:![]() 平面BDE;
平面BDE;
(2)求二面角C-EM-N的正弦值.
(3)已知点H在棱PA上,且直线NH与直线BE所成角的余弦值为![]() ,求线段AH的长.
,求线段AH的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 过点
过点 ,离心率为
,离心率为![]() .
.![]() 分别是椭圆
分别是椭圆![]() 的上、下顶点,
的上、下顶点,![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的一点.
的一点.

(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 在直线
在直线![]() 上,且
上,且![]() ,求
,求![]() 的面积;
的面积;
(3)过点![]() 作斜率为
作斜率为![]() 的直线分别交椭圆
的直线分别交椭圆![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,且点
,且点![]() 在线段
在线段![]() 上(不包括端点
上(不包括端点![]() ),直线
),直线![]() 与直线
与直线![]() 交于点
交于点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司利用简单随机抽样方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:
赔付金额(元) | 0 | 1 000 | 2 000 | 3 000 | 4 000 |
车辆数(辆) | 500 | 130 | 100 | 150 | 120 |
(1)若每辆车的投保金额均为2800元,估计赔付金额大于投保金额的概率.
(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4000元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知梯形![]() 如图(1)所示,其中
如图(1)所示,其中![]() ,
, ![]() ,四边形
,四边形![]() 是边长为
是边长为![]() 的正方形,现沿
的正方形,现沿![]() 进行折叠,使得平面
进行折叠,使得平面![]() 平面
平面![]() ,得到如图(2)所示的几何体.
,得到如图(2)所示的几何体.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)已知点![]() 在线段
在线段![]() 上,且
上,且![]() 平面
平面![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com