
ЁОЬтФПЁПФГжабЇвЛЮЛИпШ§АржїШЮЖдБОАр50УћбЇЩњбЇЯАЛ§МЋадКЭЖдД§АрМЖЙЄзїЕФЬЌЖШНјааЕїВщЃЌЕУЕНЕФЭГМЦЪ§ОнШчЯТБэЫљЪОЃК
Л§МЋВЮМгАрМЖЙЄзї | ВЛЛ§МЋВЮМгАрМЖЙЄзї | КЯМЦ | |
бЇЯАЛ§МЋадИп | 18 | 7 | 25 |
бЇЯАЛ§МЋадВЛИп | 6 | 19 | 25 |
КЯМЦ | 24 | 26 | 50 |
ЃЈ1ЃЉШчЙћЫцЛњЕїВщетИіАрЕФвЛУћбЇЩњЃЌФЧУДГщЕНВЛЛ§МЋВЮМгАрМЖЙЄзїЧвбЇЯАЛ§МЋадВЛИпЕФбЇЩњЕФИХТЪЪЧЖрЩйЃП
ЃЈ2ЃЉШєВЛЛ§МЋВЮМгАрМЖЙЄзїЧвбЇЯАЛ§МЋадИпЕФ7УћбЇЩњжагаСНУћФаЩњЃЌЯжДгжаГщШЁСНУћбЇЩњВЮМгФГЯюЛюЖЏЃЌЮЪСНУћбЇЩњжага1УћФаЩњЕФИХТЪЪЧЖрЩйЃП
ЃЈ3ЃЉбЇЩњЕФбЇЯАЛ§МЋадгыЖдД§АрМЋЙЄзїЕФЬЌЖШЪЧЗёгаЙиЯЕЃПЧыЫЕУїРэгЩ.
ИНЃК
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
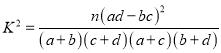
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉга99.9%ЕФАбЮе.
ЃЛЃЈ3ЃЉга99.9%ЕФАбЮе.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЫцЛњЕїВщетИіАрЕФвЛУћбЇЩњЃЌга50жжЧщПіЃЌГщЕНВЛЛ§МЋВЮМгАрМЖЙЄзїЧвбЇЯАЛ§МЋадВЛИпЕФбЇЩњЃЌга19жжЧщПіЃЌМДПЩЧѓГіИХТЪЃЛ
ЃЈ2ЃЉРћгУСаОйЗЈШЗЖЈЛљБОЪТМўЕФИіЪ§ЃЌМДПЩЧѓГіСНУћбЇЩњжага1УћФаЩњЕФИХТЪЃЛ
ЃЈ3ЃЉЧѓГі![]() ЃЌгыСйНчжЕБШНЯЃЌМДПЩЕУГіНсТлЃЎ
ЃЌгыСйНчжЕБШНЯЃЌМДПЩЕУГіНсТлЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉгЩЬтжЊЃЌВЛЛ§МЋВЮМгАрМЖЙЄзїЧвбЇЯАЛ§МЋадВЛИпЕФбЇЩњга19ШЫЃЌзмШЫЪ§ЮЊ50ШЫЃЌ
Ыљвд![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩшет7УћбЇЩњЗжБ№ЮЊ![]() ЃЈДѓаДЮЊФаЩњЃЉЃЌдђДгжаГщШЁСНУћбЇЩњЕФЧщПігаЃК
ЃЈДѓаДЮЊФаЩњЃЉЃЌдђДгжаГщШЁСНУћбЇЩњЕФЧщПігаЃК
![]() ЃЌ
ЃЌ
![]() ЃЌЙВ21жжЧщПіЃЌЦфжага1УћФаЩњЕФга10жжЧщПіЃЌ
ЃЌЙВ21жжЧщПіЃЌЦфжага1УћФаЩњЕФга10жжЧщПіЃЌ
Ёр![]() ЃЎ
ЃЎ
ЃЈ3ЃЉгЩЬтвтЕУЃЌ ![]() ЃЌЙЪга99.9%ЕФАбЮеШЯЮЊЁАбЇЩњЕФбЇЯАЛ§МЋадгыЖдД§АрМЖЙЄзїЕФЬЌЖШЁБгаЙиЯЕЃЎ
ЃЌЙЪга99.9%ЕФАбЮеШЯЮЊЁАбЇЩњЕФбЇЯАЛ§МЋадгыЖдД§АрМЖЙЄзїЕФЬЌЖШЁБгаЙиЯЕЃЎ


 ЯАЬтОЋбЁЯЕСаД№АИ
ЯАЬтОЋбЁЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃФаХЎРКЧђЖгИїга10УћЖгдБЃЌЯжНЋет20УћЖгдБЕФЩэИпЛцжЦГЩОЅвЖЭМЃЈЕЅЮЛЃК![]() ЃЉ.ФаЖгдБЩэИпдк
ЃЉ.ФаЖгдБЩэИпдк![]() вдЩЯЖЈвхЮЊЁАИпИізгЁБЃЌХЎЖгдБЩэИпдк
вдЩЯЖЈвхЮЊЁАИпИізгЁБЃЌХЎЖгдБЩэИпдк![]() вдЩЯЖЈвхЮЊЁАИпИізгЁБЃЌЦфЫћЖгдБЖЈвхЮЊЁАЗЧИпИізгЁБЃЌАДееЁАИпИізгЁБКЭЁАЗЧИпИізгЁБгУЗжВуГщбљЕФЗНЗЈЙВГщШЁ5УћЖгдБ.
вдЩЯЖЈвхЮЊЁАИпИізгЁБЃЌЦфЫћЖгдБЖЈвхЮЊЁАЗЧИпИізгЁБЃЌАДееЁАИпИізгЁБКЭЁАЗЧИпИізгЁБгУЗжВуГщбљЕФЗНЗЈЙВГщШЁ5УћЖгдБ.
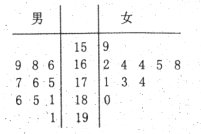
(1)Дгет5УћЖгдБжаЫцЛњбЁГі2УћЖгдБЃЌЧѓет2УћЖгдБжагаЁАИпИізгЁБЕФИХТЪЃЛ
(2)Чѓет5УћЖгдБжаЃЌЧЁКУФаХЎЁАИпИізгЁБИї1УћЖгдБЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЖдгкЖЈвхдк![]() ЩЯЕФСЌајКЏЪ§
ЩЯЕФСЌајКЏЪ§![]() ЃЌДцдкГЃЪ§
ЃЌДцдкГЃЪ§![]() ЃЈ
ЃЈ![]() ЃЉЃЌЪЙЕУ
ЃЉЃЌЪЙЕУ![]() ЖдШЮвтЕФЪЕЪ§
ЖдШЮвтЕФЪЕЪ§![]() ГЩСЂЃЌдђГЦ
ГЩСЂЃЌдђГЦ![]() ЪЧЛиа§КЏЪ§ЃЌЧвНзЪ§ЮЊ
ЪЧЛиа§КЏЪ§ЃЌЧвНзЪ§ЮЊ![]() .
.
ЃЈ1ЃЉЪдХаЖЯКЏЪ§![]() ЪЧЗёЪЧвЛИіНзЪ§ЮЊ1ЕФЛиа§КЏЪ§ЃЌВЂЫЕУїРэгЩЃЛ
ЪЧЗёЪЧвЛИіНзЪ§ЮЊ1ЕФЛиа§КЏЪ§ЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉвбжЊ![]() ЪЧЛиа§КЏЪ§ЃЌЧѓЪЕЪ§
ЪЧЛиа§КЏЪ§ЃЌЧѓЪЕЪ§![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉШєЛиа§КЏЪ§![]() ЃЈ
ЃЈ![]() ЃЉдк
ЃЉдк![]() ЧЁга100ИіСуЕуЃЌЧѓЪЕЪ§
ЧЁга100ИіСуЕуЃЌЧѓЪЕЪ§![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШє![]() ЃЌХаЖЯКЏЪ§
ЃЌХаЖЯКЏЪ§![]() ЕФЕЅЕїадЃЛ
ЕФЕЅЕїадЃЛ
ЃЈ2ЃЉШєКЏЪ§![]() дкЖЈвхгђФкЕЅЕїЕнМѕЃЌЧѓЪЕЪ§
дкЖЈвхгђФкЕЅЕїЕнМѕЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЕБ![]() ЪБЃЌЙигк
ЪБЃЌЙигк![]() ЕФЗНГЬ
ЕФЗНГЬ![]() дк
дк![]() ЩЯЧЁгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌЧѓЪЕЪ§
ЩЯЧЁгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФРтзЖ![]() ЕФЕзУцЮЊжБНЧЬнаЮЃЌ
ЕФЕзУцЮЊжБНЧЬнаЮЃЌ![]()
![]() ЃЌЦНУц
ЃЌЦНУц![]() ЕзУц
ЕзУц![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЮЊе§Ш§НЧаЮЃЌ
ЮЊе§Ш§НЧаЮЃЌ![]() ЪЧРт
ЪЧРт![]() ЩЯЕФвЛЕу(вьгкЖЫЕу).
ЩЯЕФвЛЕу(вьгкЖЫЕу).
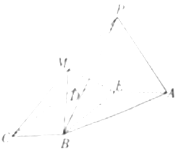
ЃЈЂёЃЉШє![]() ЮЊ
ЮЊ![]() жаЕуЃЌЧѓжЄЃК
жаЕуЃЌЧѓжЄЃК![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈЂђЃЉЪЧЗёДцдкЕу![]() ЃЌЪЙЖўУцНЧ
ЃЌЪЙЖўУцНЧ![]() ЕФДѓаЁЮЊ30Ёу.ШєДцдкЃЌЧѓГіЕу
ЕФДѓаЁЮЊ30Ёу.ШєДцдкЃЌЧѓГіЕу![]() ЕФЮЛжУЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.
ЕФЮЛжУЃЛШєВЛДцдкЃЌЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪЧЗёДцдкГЃЪ§![]() ЃЌЪЙЕШЪН
ЃЌЪЙЕШЪН![]() ЖдгквЛЧа
ЖдгквЛЧа![]() ЖМГЩСЂЃПШєВЛДцдкЃЌЫЕУїРэгЩЃЛШєДцдкЃЌЧыгУЪ§бЇЙщФЩЗЈжЄУїЃП
ЖМГЩСЂЃПШєВЛДцдкЃЌЫЕУїРэгЩЃЛШєДцдкЃЌЧыгУЪ§бЇЙщФЩЗЈжЄУїЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋЫОЮЊШЗЖЈЯТвЛФъЖШЭЖШыФГжжВњЦЗЕФаћДЋЗбЃЌашСЫНтФъаћДЋЗб![]() ЃЈЕЅЮЛЃКЧЇдЊЃЉЖдФъРћШѓ
ЃЈЕЅЮЛЃКЧЇдЊЃЉЖдФъРћШѓ![]() ЃЈЕЅЮЛЃКЭђдЊЃЉЕФгАЯьЃЌЖдНќ5ФъЕФаћДЋЗб
ЃЈЕЅЮЛЃКЭђдЊЃЉЕФгАЯьЃЌЖдНќ5ФъЕФаћДЋЗб![]() КЭФъРћШѓ
КЭФъРћШѓ![]() ЃЈ
ЃЈ![]() ЃЉНјааСЫЭГМЦЃЌСаГіСЫЯТБэЃК
ЃЉНјааСЫЭГМЦЃЌСаГіСЫЯТБэЃК
| 2 | 4 | 7 | 17 | 30 |
| 1 | 2 | 3 | 4 | 5 |
дБЙЄаЁЭѕКЭаЁРюЗжБ№ЬсЙЉСЫВЛЭЌЕФЗНАИЃЎ
ЃЈ1ЃЉаЁЭѕзМБИгУЯпадЛиЙщФЃаЭФтКЯ![]() гы
гы![]() ЕФЙиЯЕЃЌЧыФуАяжњНЈСЂ
ЕФЙиЯЕЃЌЧыФуАяжњНЈСЂ![]() Йигк
Йигк![]() ЕФЯпадЛиЙщЗНГЬЃЛЃЈЯЕЪ§ОЋШЗЕН0.01ЃЉ
ЕФЯпадЛиЙщЗНГЬЃЛЃЈЯЕЪ§ОЋШЗЕН0.01ЃЉ
ЃЈ2ЃЉаЁРюОіЖЈбЁдёЖдЪ§ЛиЙщФЃаЭФтКЯ![]() гы
гы![]() ЕФЙиЯЕЃЌЕУЕНСЫЛиЙщЗНГЬЃК
ЕФЙиЯЕЃЌЕУЕНСЫЛиЙщЗНГЬЃК![]() ЃЌВЂЬсЙЉСЫЯрЙижИЪ§
ЃЌВЂЬсЙЉСЫЯрЙижИЪ§![]() ЃЎЧыгУЯрЙижИЪ§ЫЕУїбЁдёФФИіФЃаЭИќКЯЪЪЃЌВЂдЄВтФъаћДЋЗбЮЊ4ЭђдЊЕФФъРћШѓЃЎЃЈОЋШЗЕН0.01ЃЉЃЈаЁЭѕвВЬсЙЉСЫЫћЕФЗжЮіЗжЮіЪ§Он
ЃЎЧыгУЯрЙижИЪ§ЫЕУїбЁдёФФИіФЃаЭИќКЯЪЪЃЌВЂдЄВтФъаћДЋЗбЮЊ4ЭђдЊЕФФъРћШѓЃЎЃЈОЋШЗЕН0.01ЃЉЃЈаЁЭѕвВЬсЙЉСЫЫћЕФЗжЮіЗжЮіЪ§Он![]() ЃЉ
ЃЉ
ВЮПМЙЋЪНЃКЯрЙижИЪ§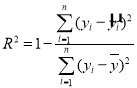
ЛиЙщЗНГЬ![]() жааБТЪКЭНиОрЕФзюаЁЖўГЫЙРМЦЙЋЪНЗжБ№ЮЊЃК
жааБТЪКЭНиОрЕФзюаЁЖўГЫЙРМЦЙЋЪНЗжБ№ЮЊЃК
 ЃЌ
ЃЌ![]() ЃЎВЮПМЪ§ОнЃК
ЃЎВЮПМЪ§ОнЃК![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]()
ЃЈЂёЃЉЕБa=Љ2ЪБЃЌЧѓКЏЪ§f(x)ЕФЕЅЕїЧјМфЃЛ
ЃЈЂђЃЉШєg(x)= ![]() +
+![]() дк
дк![]() 1ЃЌ+Ёо)ЩЯЪЧЕЅЕїКЏЪ§ЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇ.
1ЃЌ+Ёо)ЩЯЪЧЕЅЕїКЏЪ§ЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЁао4-5ЃКВЛЕШЪНбЁНВ
вбжЊКЏЪ§![]() .
.
ЃЈIЃЉЧѓжЄЃК![]() КуГЩСЂЃЛ
КуГЩСЂЃЛ
ЃЈIIЃЉШєДцдкЪЕЪ§![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌЧѓЪЕЪ§
ЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com