Question

【题目】如图1,在直角梯形ABCD中,AD∥BC,∠BAD=,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图2.

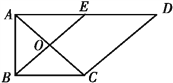
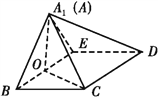
　　　　　图1　　　　　　　　　　　　　图2

(1)证明:CD⊥平面A1OC;

(2)若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD夹角的余弦值.

Answer 1

【答案】(1) 见解析；(2)

【解析】试题分析：（1）折起后， 根据线面垂直的判定定理可得平面，即可证明平面；（2）若平面平面，根据（1）可得 两两垂直，以 建立空间坐标系，利用向量垂直数量积为零，分别求出平面与平面的法向量，根据空间向量夹角余弦公式可得结果.

试题解析：(1) 在题图1中,因为AB=BC=1,AD=2,E是AD的中点,∠BAD= AD∥BC,

所以BE⊥AC,BE∥CD,

即在题图2中,BE⊥OA1,BE⊥OC,且OA1∩OC=O,

从而BE⊥平面A1OC,

又CD∥BE,

所以CD⊥平面A1OC.

(2)解:因为平面A1BE⊥平面BCDE,

又由(1)知BE⊥OA1,BE⊥OC,

所以∠A1OC为二面角A1BEC的平面角,

所以∠A1OC=.

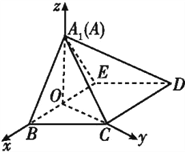
如图,以O为原点,建立空间直角坐标系,

因为A1B=A1E=BC=ED=1,

BC∥ED,

所以B

（,0,0）,E（- ,0,0）,

A1（0,0, ）,C（0, ,0）,

得=（-, ,0）, =（0, ,- ）,

= (-,0,0).

设平面A1BC的法向量n1=(x1,y1,z1),

平面A1CD的法向量n2=(x2,y2,z2),平面A1BC与平面A1CD夹角为θ,

则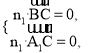

得

取n1=(1,1,1);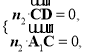

得

取n2=(0,1,1),

从而cos θ=|cos<n1,n2>|= =,

即平面A1BC与平面A1CD夹角的余弦值为.