
【题目】设数列![]() 的前
的前![]() 项的和为
项的和为![]() 且
且![]() 数列
数列![]() 满足
满足![]() 且对任意正整数
且对任意正整数![]() 都有
都有![]() 成等比数列.
成等比数列.
(1)求数列![]() 的通项公式.
的通项公式.
(2)证明数列![]() 为等差数列.
为等差数列.
(3)令![]() 问是否存在正整数
问是否存在正整数![]() 使得
使得![]() 成等比数列?若存在,求出
成等比数列?若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
【答案】(1)![]() (2)见证明;(3)见证明
(2)见证明;(3)见证明
【解析】
(1)利用项和公式求数列![]() 的通项公式.(2)由题得
的通项公式.(2)由题得![]() ,
,![]() ,即
,即![]() ,再求出
,再求出![]() ,再利用等差数列的定义证明数列
,再利用等差数列的定义证明数列![]() 为等差数列.(3) 先求出
为等差数列.(3) 先求出![]() ,所以
,所以![]() ,根据
,根据![]() 成等比数列得
成等比数列得![]() ,即
,即![]() ,再求出m,k的值.
,再求出m,k的值.
(1)因为数列![]() 的前
的前![]() 项的和
项的和![]() ,
,
所以当![]() 时,
时,![]() ;
;
当![]() 且
且![]() 时,
时,![]() ,
,
当![]() 时,上式也成立,
时,上式也成立,
所以数列![]() 的通项公式为
的通项公式为![]() .
.
(2)证明:因为对任意正整数![]() 都有
都有![]() 成等比数列,
成等比数列,
所以![]() ,即
,即![]() ,
,
所以![]() ,
,
两式相除得,对任意正整数![]() 都有
都有![]() ,
,
即![]() ,
,
当![]() 为奇数时,
为奇数时,![]() ,所以
,所以![]() ,
,
当![]() 为偶数时,
为偶数时,![]() ,而
,而![]() ,所以
,所以![]() ,
,
所以![]() .
.
所以![]() ,
,
所以数列![]() 为等差数列.
为等差数列.
(3)因为![]() ,
,
所以![]() ,
,
因此存在正整数![]() ,使得
,使得![]() 成等比数列
成等比数列
![]()
![]() ,
,
![]()
因为![]() 都是正整数,则
都是正整数,则![]() ,
,
即![]() 时,对应的
时,对应的![]() .
.
所以存在![]() 或
或![]() 或
或![]() 使得
使得![]() 成等比数列.
成等比数列.


科目:高中数学 来源: 题型:
【题目】某单位有员工1000名,平均每人每年创造利润10万元.为增加企业竞争力,决定优化产业结构,调整出![]() 名员工从事第三产业,调整后平均每人每年创造利润为
名员工从事第三产业,调整后平均每人每年创造利润为![]() 万元
万元![]() ,剩下的员工平均每人每年创造的利润可以提高
,剩下的员工平均每人每年创造的利润可以提高![]() .
.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(2)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润条件下,若要求调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,则![]() 的取值范围是多少?
的取值范围是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
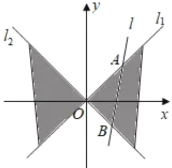
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与直线
与直线![]() 之间的阴影部分记为
之间的阴影部分记为![]() ,区域
,区域![]() 中动点
中动点![]() 到
到![]() 的距离之积为1.
的距离之积为1.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)对于区域![]() 中动点
中动点![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)动直线![]() 穿过区域
穿过区域![]() ,分别交直线
,分别交直线![]() 于
于![]() 两点,若直线
两点,若直线![]() 与点
与点![]() 的轨迹
的轨迹![]() 有且只有一个公共点,求证:
有且只有一个公共点,求证:![]() 的面积值为定值.
的面积值为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的图象的顶点坐标为
的图象的顶点坐标为![]() ,且过坐标原点
,且过坐标原点![]() .数列
.数列![]() 的前
的前![]() 项和为
项和为![]() ,点
,点![]() 在二次函数
在二次函数![]() 的图象上.
的图象上.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)在数列![]() 中是否存在这样一些项:
中是否存在这样一些项:![]()
![]()
![]() ,这些项都能够构成以
,这些项都能够构成以![]() 为首项,
为首项,![]() 为公比的等比数列
为公比的等比数列![]() ?若存在,写出
?若存在,写出![]() 关于
关于![]() 的表达式;若不存在,说明理由.
的表达式;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
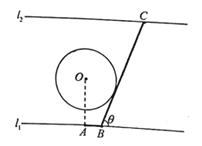
【题目】如图为某大河的一段支流,岸线![]() 近似满足
近似满足![]() ∥
∥![]() 宽度为7
宽度为7![]() 圆
圆![]() 为河中的一个半径为2
为河中的一个半径为2![]() 的小岛,小镇
的小岛,小镇![]() 位于岸线
位于岸线![]() 上,且满足岸线
上,且满足岸线![]() 现计划建造一条自小镇
现计划建造一条自小镇![]() 经小岛
经小岛![]() 至对岸
至对岸![]() 的通道
的通道![]() (图中粗线部分折线段,
(图中粗线部分折线段,![]() 在
在![]() 右侧),为保护小岛,
右侧),为保护小岛,![]() 段设计成与圆
段设计成与圆![]() 相切,设
相切,设![]()
(1)试将通道![]() 的长
的长![]() 表示成
表示成![]() 的函数,并指出其定义域.
的函数,并指出其定义域.
(2)求通道![]() 的最短长.
的最短长.
查看答案和解析>>
科目:高中数学 来源: 题型:
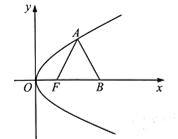
【题目】在平面直角坐标系![]() 中,已知点F为抛物线
中,已知点F为抛物线![]() 的焦点,点A在抛物线E上,
的焦点,点A在抛物线E上,
点B在x轴上,且![]() 是边长为2的等边三角形。
是边长为2的等边三角形。
(1)求抛物线E的方程;
(2)设C是抛物线E上的动点,直线![]() 为抛物线E在点C处的切线,求点B到直线
为抛物线E在点C处的切线,求点B到直线![]() 距离的最小值,并求此时点C的坐标。
距离的最小值,并求此时点C的坐标。
查看答案和解析>>
科目:高中数学 来源: 题型:
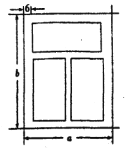
【题目】如图,一个铝合金窗分为上、下两栏,四周框架和中间隔档的材料为铝合金,宽均为6![]() ,上栏与下栏的框内高度(不含铝合金部分)的比为1:2,此铝合金窗占用的墙面面积为28800
,上栏与下栏的框内高度(不含铝合金部分)的比为1:2,此铝合金窗占用的墙面面积为28800![]() ,设该铝合金窗的宽和高分别为
,设该铝合金窗的宽和高分别为![]() ,铝合金窗的透光部分的面积为
,铝合金窗的透光部分的面积为![]() .
.
(1)试用![]() 表示
表示![]() ;
;
(2)若要使![]() 最大,则铝合金窗的宽和高分别为多少?
最大,则铝合金窗的宽和高分别为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com