
 如图,给定单位向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°,点C在以O为圆心的$\widehat{AB}$上运动.若$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$,其中x,y∈R,则x+2y的最大值是$\frac{2\sqrt{21}}{3}$.
如图,给定单位向量$\overrightarrow{OA}$和$\overrightarrow{OB}$,它们的夹角为120°,点C在以O为圆心的$\widehat{AB}$上运动.若$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$,其中x,y∈R,则x+2y的最大值是$\frac{2\sqrt{21}}{3}$. 分析 根据题意,建立直角坐标系,设出∠AOC=α,用cosα,sinα表示出$\overrightarrow{OC}$,由此求出x,y的值,再利用三角函数求x+2y的最大值.
解答 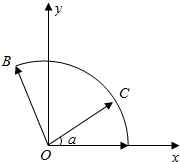 解:根据题意,建立如图所示的坐标系,
解:根据题意,建立如图所示的坐标系,
则A(1,0),B(cos120°,sin120°),
即B(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$);
设∠AOC=α,则$\overrightarrow{OC}$=(cosα,sinα),
∵$\overrightarrow{OC}=x\overrightarrow{OA}+y\overrightarrow{OB}$,
∴(cosα,sinα)=(x,0)+(-$\frac{1}{2}$y,$\frac{\sqrt{3}}{2}$y);
即cosα=x-$\frac{1}{2}$y,sinα=$\frac{\sqrt{3}}{2}$y,
解得:x=$\frac{\sqrt{3}}{3}$sinα+cosα,y=$\frac{2\sqrt{3}}{3}$sinα;
∴x+2y=$\frac{5\sqrt{3}}{3}$sinα+cosα=$\frac{2\sqrt{21}}{3}$sin(α+θ),其中tanθ=$\frac{\sqrt{3}}{5}$;
又sin(α+θ)≤1,
∴x+2y≤$\frac{2\sqrt{21}}{3}$.
故答案为:$\frac{2\sqrt{21}}{3}$.
点评 本题考查了平面向量知识的运用问题,也考查了三角函数的应用问题,解题的关键是确定x,y的关系式,是中档题目.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,1.25) | B. | (1.25,1.5) | C. | (1.5,2) | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )| A. | 91 5.5 | B. | 91 5 | C. | 92 5.5 | D. | 92 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com