
【题目】已知函数f(x)=cos2x+2 ![]() sinxcosx﹣sin2x.
sinxcosx﹣sin2x.
(1)求函数f(x)的最小正周期
(2)求函数f(x)单调增区间.
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi , yi)(i=1,2,…,n),用最小二乘法建立的回归方程为: ![]() =0.85x﹣85.71,则下列结论中不正确的是( )
=0.85x﹣85.71,则下列结论中不正确的是( )
A.3与3x2+2ax+b=0具有正的线性相关关系
B.回归直线过样本点的中心( ![]() ,
, ![]() )
)
C.若该大学某女生身高为170cm,则可断定其体重必为58.79kg
D.若该大学某女生身高增加1cm,则其体重约增加0.85kg
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间将10名技工平均分成甲、乙两组加工某种零件,在单位时间内每个技工加工的合格零件数的统计数据的茎叶图如图所示.已知两组技工在单位时间内加工的合格零件平均数都为9.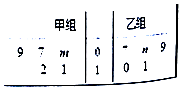
(1)分别求出m,n的值;
(2)分别求出甲、乙两组技工在单位时间内加工的合格零件的方差s甲2和s乙2 , 并由此分析两组技工的加工水平.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)的导函数y=f′(x)的图象如图,则( ) 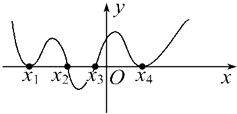
A.函数f(x)有1个极大值点,1个极小值点
B.函数f(x)有2个极大值点,2个极小值点
C.函数f(x)有3个极大值点,1个极小值点
D.函数f(x)有1个极大值点,3个极小值点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设y=f(x)是二次函数,方程f(x)=0有两个相等的实根,且f′(x)=2x﹣2.
(1)求y=f(x)的表达式;
(2)求y=f(x)的图象与两坐标轴所围成封闭图形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且Sn=2an﹣3n(n∈N+).
(1)求a1 , a2 , a3的值;
(2)设bn=an+3,证明数列{bn}为等比数列,并求通项公式an .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=2px(p>0)
(1)若直线x﹣y﹣2=0过抛物线C的焦点,求抛物线C的方程,并求出准线方程;
(2)设p=2,A,B是C上异于坐标原点O的两个动点,满足OA⊥OB,△ABO的面积是否存在最小值?若存在,请求出最小值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com