练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．在圆中直径所对的圆周角是直角，有同学类比圆研究椭圆，把经过椭圆中心的弦叫做椭圆的直径．已知椭圆
    C：$\frac{{x}^{2}}{3}$+y2=1，AB是椭圆C的直径．
    （I ）求椭圆C的离心率；
    （Ⅱ）该同学用几何画板在椭圆C上取了几个点．通过测量发现毎一个点与A，B连线的斜率之积不变．耶么对于椭圆上任意一点M（M不与A，B重合），直线MA，MB的斜率之积是否为定值．若是．写出定值并证明你的结论；若不是请说明理由．
    （III）O是坐标原点，M是椭圆上的一点且在第一象限．M关于原点的对称点为M′，E是x轴一点．△MOE是等等腰三角形．MO=ME，直线M′E与椭圆的另一个交点为N，求证：∠M′MN是直角．

    分析 （Ⅰ）求出椭圆的a，b，c，由e=$\frac{c}{a}$，计算可得；
    （Ⅱ）直线MA，MB的斜率之积为定值-$\frac{1}{3}$．设M（m，n），A（s，t），B（-s，-t），代入椭圆方程，相减，再由直线的斜率公式，化简整理可得结论；
    （III）设M（m，n）（m＞0，n＞0），M'（-m，-n），E（g，0），N（u，v），由题意可得kMO+kME=0，求出E的坐标，直线M'E的方程，代入椭圆方程，运用韦达定理，求得N的坐标，再由向量$\overrightarrow{M'M}$，$\overrightarrow{MN}$的数量积的坐标表示，化简整理，即可得证．

    解答 解：（Ⅰ）椭圆C：$\frac{{x}^{2}}{3}$+y2=1的a=$\sqrt{3}$，b=1，c=$\sqrt{{a}^{2}-{b}^{2}}$=$\sqrt{2}$，
    可得椭圆C的离心率为e=$\frac{c}{a}$=$\frac{\sqrt{6}}{3}$；
    （Ⅱ）直线MA，MB的斜率之积为定值-$\frac{1}{3}$．
    理由：设M（m，n），A（s，t），B（-s，-t），
    则$\frac{{m}^{2}}{3}$+n2=1，$\frac{{s}^{2}}{3}$+t2=1，
    相减可得，$\frac{{m}^{2}-{s}^{2}}{3}$=-（n2-t2），
    即有kMA•kMB=$\frac{n-t}{m-s}$•$\frac{n+t}{m+s}$=$\frac{{n}^{2}-{t}^{2}}{{m}^{2}-{s}^{2}}$=-$\frac{1}{3}$；
    （Ⅲ）证明：设M（m，n）（m＞0，n＞0），M'（-m，-n），E（g，0），N（u，v），
    由△MOE是等等腰三角形．MO=ME，可得kMO+kME=0，
    即为$\frac{n}{m}$+$\frac{n}{m-g}$=0，可得g=2m，即E（2m，0），
    直线M'E：y=$\frac{n}{3m}$（x-2m），代入椭圆x2+3y2=3，
    可得（1+$\frac{{n}^{2}}{3{m}^{2}}$）x2-$\frac{4{n}^{2}}{3m}$x+$\frac{4{n}^{2}}{3}$-3=0，
    可得-m+u=$\frac{4m{n}^{2}}{{n}^{2}+3{m}^{2}}$，解得u=$\frac{5m{n}^{2}+3{m}^{3}}{{n}^{2}+3{m}^{2}}$，
    v=$\frac{n}{3m}$（u-2m）=$\frac{n（{n}^{2}-{m}^{2}）}{{n}^{2}+3{m}^{2}}$，
    则$\overrightarrow{M'M}$•$\overrightarrow{MN}$=（2m，2n）•（u-m，v-n）=2mu-2m2+2nv-2n2
    =$\frac{2m（5m{n}^{2}+3{m}^{3}）}{{n}^{2}+3{m}^{2}}$-2m2+$\frac{2{n}^{2}（{n}^{2}-{m}^{2}）}{{n}^{2}+3{m}^{2}}$-2n2
    =$\frac{8{m}^{2}{n}^{2}}{{n}^{2}+3{m}^{2}}$+$\frac{-8{m}^{2}{n}^{2}}{{n}^{2}+3{m}^{2}}$=0．
    即有$\overrightarrow{M'M}$⊥$\overrightarrow{MN}$，
    则∠M′MN是直角．

    点评 本题考查椭圆的方程和性质，主要是离心率和方程的运用，考查联立方程相减，消元，运用韦达定理，考查向量垂直的条件：数量积为0，同时考查直线的斜率和方程的运用，考查化简整理的运算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    13．已知曲线C的极坐标方程为ρ=-2sinθ，则其直角坐标方程为x2+（y+1）2=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．双曲线C的左，右焦点分别为F1（-1，0），F2（1，0），抛物线y2=4x与双曲线C的一个交点为P，若（$\overrightarrow{{F}_{2}P}$+$\overrightarrow{{F}_{2}{F}_{1}}$）•（$\overrightarrow{{F}_{2}P}$-$\overrightarrow{{F}_{2}{F}_{1}}$）=0，则C的离心率为（　　）
    A．$\sqrt{2}$B．1+$\sqrt{2}$C．1+$\sqrt{3}$D．2+$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知复数z满足1+i=（1-i）2z，则z的共轭复数在复平面内所对应的点位于（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．为检测空气质量，某市环保局随机抽取了甲、乙两地2016年20天PM2.5日平均浓度（单位：微克/立方米）监测数据，得到甲地PM2.5日平均浓度频率分布直方图和乙地PM2.5日平均浓度的频数分布表．

    乙地20天PM2.5日平均浓度频数分布表
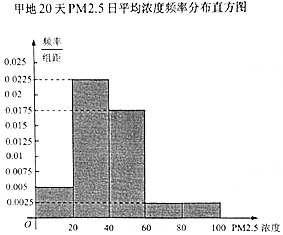
    PM2.5日平均浓度（微克/立方米）[0，20]（20，40]（40，60]（60，80]（80，100]
    频数（天）23465
    （1）根据乙地20天PM2.5日平均浓度的频率分布表，作出作出相应的频率分组直方图，并通过两个频率分布直方图比较两地PM2.5日平均浓度的平均值及分散程度（不要求计算出具体值，给出结论即可）；
    （2）通过调查，该市市民对空气质量的满意度从高到低分为三个等级：
    满意度等级非常满意满意不满意
    PM2.5日平均浓度（微克/立方米）不超过20大于20不超过60超过60
    从乙地这20天PM2.5日平均浓度不超过40的天数中随机抽取两天，求这两天中至少有一天居民对空气质量满意度为“非常满意”的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）=x2-1+aln（1-x），a∈R．
    （Ⅰ）若函数f（x）为定义域上的单调函数，求实数a的取值范围；
    （Ⅱ）若函数f（x）存在两个极值点x1，x2，且x1＜x2．证明：$\frac{f（{x}_{1}）}{{x}_{2}}$＞$\frac{f（{x}_{2}）}{{x}_{1}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．若复数z=2-i+i2，则z2=（　　）
    A．2B．2iC．-2iD．$\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．圆ρ=r与圆ρ=-2rsin（θ+$\frac{π}{4}$）（r＞0）的公共弦所在直线的方程为（　　）
    A．2ρ（sin θ+cos θ）=rB．2ρ（sin θ+cos θ）=-r
    C．$\sqrt{2}$ρ（sin θ+cos θ）=rD．$\sqrt{2}$ρ（sin θ+cos θ）=-r

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知x，y∈R，则“xy＜1是“0＜x＜$\frac{1}{y}$”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    同步练习册答案