【题目】已知点
为抛物线
： 
的焦点，点
是准线
上的动点，直线
交抛物线
于
两点，若点
的纵坐标为
，点
为准线
与
轴的交点.
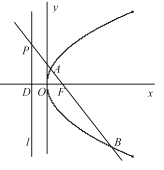
（1）求直线
的方程；
（2）求
的面积
范围.
科目：高中数学 来源： 题型：
【题目】如图，动点P从单位正方形ABCD顶点A开始，顺次经B、C、D绕边界一周，当
表示点P的行程， 
表示PA之长时，求y关于x的解析式，并求
的值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，PA垂直于以AB为直径的圆所在平面，C为圆上异于A，B的任意一点，
垂足为E，点F是PB上一点，则下列判断中不正确的是（ ）﹒
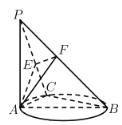
A.
平面PACB.
C.
D.平面
平面PBC
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，已知圆
，圆
.
（1）若过点
的直线
被圆
截得的弦长为
，求直线的方程；
（2）设动圆
同时平分圆
的周长、圆的周长.
①证明：动圆圆心在一条定直线上运动；
②动圆是否经过定点？若经过，求出定点的坐标；若不经过，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知抛物线
的焦点为F，且过点A (2，2)，椭圆
的离心率为
，点B为抛物线C与椭圆D的一个公共点，且
.
(Ⅰ)求椭圆D的方程；
(Ⅱ)过椭圆内一点P(0，t)的直线l的斜率为k，且与椭圆C交于M，N两点，设直线OM，ON(O为坐标原点)的斜率分别为k1，k2，若对任意k，存在实数λ，使得k1+ k2=λk，求实数λ的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在△ABC中，已知CA=1，CB=2，∠ACB=60°．
（1）求|
|；
（2）已知点D是AB上一点，满足
=λ，点E是边CB上一点，满足
=λ
．
①当λ=
时，求
；
②是否存在非零实数λ，使得⊥？若存在，求出的λ值；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】中国第一高摩天轮“南昌之星摩天轮”高度为
，其中心
距地面
，半径为
，若某人从最低点
处登上摩天轮，摩天轮匀速旋转，那么此人与地面的距离将随时间
变化，
后达到最高点，从登上摩天轮时开始计时.
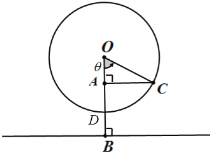
（1）求出人与地面距离
与时间的函数解析式；
（2）从登上摩天轮到旋转一周过程中，有多长时间人与地面距离大于
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某书店销售刚刚上市的某高二数学单元测试卷，按事先拟定的价格进行5天试销，每种单价试销1天，得到如下数据：
单价x/元 | 18 | 19 | 20 | 21 | 22 |
销量y/册 | 61 | 56 | 50 | 48 | 45 |
（1）求试销
天的销量的方差和
关于
的回归直线方程；
附：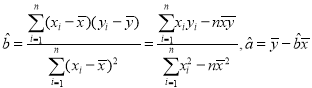 
.
（2）预计以后的销售中，销量与单价服从上题中的回归直线方程，已知每册单元测试卷的成本是10元，为了获得最大利润，该单元测试卷的单价应定为多少元？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
