
【题目】某省从2021年开始,高考采用取消文理分科,实行“![]() ”的模式,其中的“1”表示每位学生必须从物理、历史中选择一个科目且只能选择一个科目.某校高一年级有2000名学生(其中女生900人).该校为了解高一年级学生对“1”的选课情况,采用分层抽样的方法抽取了200名学生进行问卷调查,下表是根据调查结果得到的
”的模式,其中的“1”表示每位学生必须从物理、历史中选择一个科目且只能选择一个科目.某校高一年级有2000名学生(其中女生900人).该校为了解高一年级学生对“1”的选课情况,采用分层抽样的方法抽取了200名学生进行问卷调查,下表是根据调查结果得到的![]() 列联表.
列联表.
性别 | 选择物理 | 选择历史 | 总计 |
男生 | ________ | 50 |
|
女生 | 30 | ________ |
|
总计 | ________ | ________ | 200 |
(1)求![]() ,
,![]() 的值;
的值;
(2)请你依据该列联表判断是否有99.5%的把握认为选择科目与性别有关?说明你的理由.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附: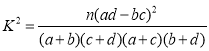 ,其中
,其中![]() .
.
科目:高中数学 来源: 题型:
【题目】已知![]() 为等差数列,各项为正的等比数列
为等差数列,各项为正的等比数列![]() 的前n项和为
的前n项和为![]() , ,且
, ,且![]() ,
,![]() ,.在①
,.在①![]() ;②
;②![]() ;③
;③![]() 这三个条件中任选其中一个,补充在上面的横线上,并完成下面问题的解答(如果选择多个条件解答,则按选择第一个解答计分).
这三个条件中任选其中一个,补充在上面的横线上,并完成下面问题的解答(如果选择多个条件解答,则按选择第一个解答计分).
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点.
两点.
(1)求过![]() 、
、![]() 、
、![]() 三点的圆
三点的圆![]() 的方程;
的方程;
(2)若![]() 为坐标原点,直线
为坐标原点,直线![]() 与椭圆
与椭圆![]() 和(1)中的圆
和(1)中的圆![]() 分别相切于点
分别相切于点![]() 和点
和点![]() (
(![]() 、
、![]() 不重合),求直线
不重合),求直线![]() 与直线
与直线![]() 的斜率之积.
的斜率之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“熔喷布”是口罩生产的重要原材料,1吨熔喷布大约可供生产100万只口罩.2020年,制造口罩的企业甲的熔喷布1月份的需求量为100吨,并且从2月份起,每月熔喷布的需求量均比上个月增加10%.企业乙是企业甲熔喷布的唯一供应商,企业乙2020年1月份的产能为100吨,为满足市场需求,从2月份到![]() 月份(
月份(![]() 且
且![]() ),每个月比上个月增加一条月产量为50吨的生产线投入生产,从
),每个月比上个月增加一条月产量为50吨的生产线投入生产,从![]() 月份到9月份不再增加新的生产线.计划截止到9月份,企业乙熔喷布的总产量除供应企业甲的需求外,还剩余不少于990吨的熔喷布可供给其它厂商,则企业乙至少要增加___条熔喷布生产线.
月份到9月份不再增加新的生产线.计划截止到9月份,企业乙熔喷布的总产量除供应企业甲的需求外,还剩余不少于990吨的熔喷布可供给其它厂商,则企业乙至少要增加___条熔喷布生产线.
(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】非典和新冠肺炎两场疫情告诉我们:应坚决杜绝食用野生动物,提倡文明健康,绿色环保的生活方式.在我国抗击新冠肺炎期间,某校开展一次有关病毒的网络科普讲座.高三年级男生60人,女生40人参加.按分层抽样的方法,在100名同学中选出5人,则男生中选出________人.再从此5人中选出两名同学作为联络人,则这两名联络人中男女都有的概率是________.(第1空2分,第2空3分)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)函数![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(2)曲线![]() 在点
在点![]() 处的切线为
处的切线为![]() ,是否存在这样的点
,是否存在这样的点![]() 使得直线
使得直线![]() 与曲线
与曲线![]() 也相切,若存在,判断满足条件的点
也相切,若存在,判断满足条件的点![]() 的个数,若不存在,请说明理由.
的个数,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某基地蔬菜大棚采用无土栽培方式种植各类蔬菜.根据过去50周的资料显示,该基地周光照量![]() (小时)都在30小时以上,其中不足50小时的有5周,不低于50小时且不超过70小时的有35周,超过70小时的有10周.根据统计,该基地的西红柿增加量
(小时)都在30小时以上,其中不足50小时的有5周,不低于50小时且不超过70小时的有35周,超过70小时的有10周.根据统计,该基地的西红柿增加量![]() (千克)与使用某种液体肥料的质量
(千克)与使用某种液体肥料的质量![]() (千克)之间的关系如图所示.
(千克)之间的关系如图所示.
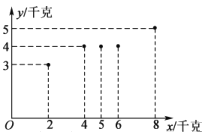
(1)依据上图,是否可用线性回归模型拟合![]() 与
与![]() 的关系?请计算相关系数
的关系?请计算相关系数![]() 并加以说明(精确到0.01).(若
并加以说明(精确到0.01).(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
(2)蔬菜大棚对光照要求较大,某光照控制仪商家为该基地提供了部分光照控制仪,但每周光照控制仪运行台数受周光照量![]() 限制,并有如下关系:
限制,并有如下关系:
周光照量 |
|
|
|
光照控制仪运行台数 | 3 | 2 | 1 |
若某台光照控制仪运行,则该台光照控制仪周利润为3000元;若某台光照控制仪未运行,则该台光照控制仪周亏损1000元.以频率作为概率,商家欲使周总利润的均值达到最大,应安装光照控制仪多少台?
附:相关系数公式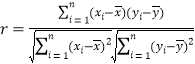 ,
,
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com