
 一个四面体的顶点都在球面上,它们的正视图、侧视图、俯视图都是右图.图中圆内有一个以圆心为中心边长为1的正方形.则这个四面体的外接球的表面积是( )
一个四面体的顶点都在球面上,它们的正视图、侧视图、俯视图都是右图.图中圆内有一个以圆心为中心边长为1的正方形.则这个四面体的外接球的表面积是( )| A、π | B、3π | C、4π | D、6π |
科目:高中数学 来源: 题型:
| OA′ |
| AA′ |
| OB′ |
| BB′ |
| OC′ |
| CC′ |
| OA′ |
| AA′ |
| OB′ |
| BB′ |
| OC′ |
| CC′ |
| S△OBC |
| S△ABC |
| S△OCA |
| S△ABC |
| S△OAB |
| S△ABC |
| S△ABC |
| S△ABC |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| t |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| a |
| b |
| 16 |
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
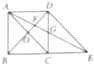 对于向量
对于向量| PAi |
| PA1 |
| PA2 |
| PAn |
| A、点A,C的“平衡点”必为点O |
| B、点D,C,E的“平衡点”为线段DE的中点 |
| C、点A,F,G,E的“平衡点”存在且唯一 |
| D、点A,B,E,D的“平衡点”必在点F |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知{an}是公差不为0的等差数列,a1=3,现将数列{an}的各项依次放入如图表格中,其中第1行1项,第2行2项,…,第n行2n-1项,记第n行各项的和为Tn,且T1,T2,T3成等比数列.数列{an}的通项公式是( )
已知{an}是公差不为0的等差数列,a1=3,现将数列{an}的各项依次放入如图表格中,其中第1行1项,第2行2项,…,第n行2n-1项,记第n行各项的和为Tn,且T1,T2,T3成等比数列.数列{an}的通项公式是( )| A、an=2n+1 |
| B、an=3n |
| C、an=4n-1 |
| D、an=2n-1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com