Question

求与圆C：（x+1）²+y²=4相切，且过点（3，0）的直线的一般方程．

Answer 1

【答案】分析：设出过点（3，0）的直线的点斜式方程，利用圆心到直线的距离等于半径，求出直线的斜率，即可求出直线的方程．
解答：解：圆C：（x+1）²+y²=4的圆心（-1，0）半径为2，
所以过点（3，0）的切线方程为y=k（x-3）．
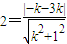
因为直线与圆相切，，解得k=，
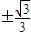
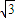
所以与圆C：（x+1）²+y²=4相切，且过点（3，0）的直线的一般方程：x±y-3=0
点评：本题是基础题，考查直线与圆相切的直线方程的求法，利用圆心到直线的距离等于半径是解题的关键，考查计算能力．