
【题目】从甲地到乙地沿某条公路行驶一共200公里,遇到红灯个数的概率如下表所示:
红灯个数 | 0 | 1 | 2 | 3 | 4 | 5 | 6个及6个以上 |
概率 | 0.02 | 0.1 |
| 0.35 | 0.2 | 0.1 | 0.03 |
(1)求表中字母![]() 的值;
的值;
(2)求至少遇到4个红灯的概率;
(3)求至多遇到5个红灯的概率.
科目:高中数学 来源: 题型:
【题目】某市组织高三全体学生参加计算机操作比赛,等级分为1至10分,随机调阅了A、B两所学校各60名学生的成绩,得到样本数据如下:
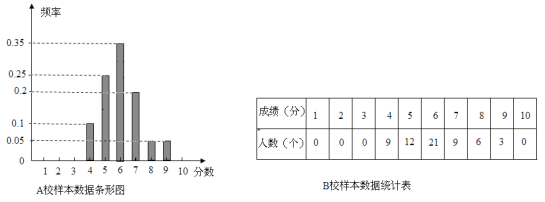
(1)计算两校样本数据的均值和方差,并根据所得数据进行比较.
(2)从A校样本数据成绩分别为7分、8分和9分的学生中按分层抽样方法抽取6人,若从抽取的6人中任选2人参加更高一级的比赛,求这2人成绩之和大于或等于15的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1的方程为![]() ,双曲线C2的左、右焦点分别是C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点,O为坐标原点.
,双曲线C2的左、右焦点分别是C1的左、右顶点,而C2的左、右顶点分别是C1的左、右焦点,O为坐标原点.
(1)求双曲线C2的方程;
(2)若直线l:y=kx+![]() 与双曲线C2恒有两个不同的交点A和B,且
与双曲线C2恒有两个不同的交点A和B,且![]() ,求k的取值范围.
,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(5分)《九章算术》“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,则第五节的容积为( )
A. 1升 B. ![]() 升 C.
升 C. ![]() 升 D.
升 D. ![]() 升
升
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个正方形花圃被分成5份.

(1)若给这5个部分种植花,要求相邻两部分种植不同颜色的花,己知现有红、黄、蓝、绿4种颜色不同的花,求有多少种不同的种植方法?
(2)若向这5个部分放入7个不同的盆栽,要求每个部分都有盆栽,问有多少种不同的放法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆C:![]() (a>b>0)的左、右焦点分别为
(a>b>0)的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,过焦点
,过焦点![]() 且垂直于x轴的直线被椭圆C截得的线段长为1.
且垂直于x轴的直线被椭圆C截得的线段长为1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)已知点M(0,-1),直线l经过点N(2,1)且与椭圆C相交于A,B两点(异于点M),记直线MA的斜率为![]() ,直线MB的斜率为
,直线MB的斜率为![]() ,证明
,证明![]() 为定值,并求出该定值.
为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校有微机![]() 台,分别放在
台,分别放在![]() 个房间,各房间开门钥匙互不相同.某期培训班有学员
个房间,各房间开门钥匙互不相同.某期培训班有学员![]() 人(
人(![]() ),每晚恰有
),每晚恰有![]() 人进机房实习操作,为保证每人一台机,至少应准备多少把钥匙分给这
人进机房实习操作,为保证每人一台机,至少应准备多少把钥匙分给这![]() 个学员,使得每晚不论哪
个学员,使得每晚不论哪![]() 个人进机房,都能用自己分到的钥匙打开一间机房的门进去练习,并按分得钥匙少的人先开门的原则,能保证每人恰可得到一个房间.
个人进机房,都能用自己分到的钥匙打开一间机房的门进去练习,并按分得钥匙少的人先开门的原则,能保证每人恰可得到一个房间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为直角梯形,BC∥AD,AB⊥BC,∠ADC=45°,PA⊥平面ABCD,AB=AP=1,AD=3.
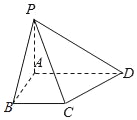
(1)求异面直线PB与CD所成角的大小;
(2)求点D到平面PBC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,BC边上的高所在直线的方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0.若点B的坐标为(1,2),求点A和点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com