
【题目】双曲线E: ![]() =1(a>0,b>0)的左、右焦点分别为F1、F2 , P是E坐支上一点,且|PF1|=|F1F2|,直线PF2与圆x2+y2=a2相切,则E的离心率为 .
=1(a>0,b>0)的左、右焦点分别为F1、F2 , P是E坐支上一点,且|PF1|=|F1F2|,直线PF2与圆x2+y2=a2相切,则E的离心率为 .
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】从1、2、3、4、5五个数字中任意取出无重复的3个数字.
(I)可以组成多少个三位数?
(II)可以组成多少个比300大的偶数?
(III)从所组成的三位数中任取一个,求该数字是大于300的奇数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,函数
,函数![]() ,
,![]() 是函数
是函数![]() 的导函数,
的导函数, ![]() 是自然对数的底数.
是自然对数的底数.
(1)当![]() 时,求导函数
时,求导函数![]() 的最小值;
的最小值;
(2)若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的最大值;
的最大值;
(3)若函数![]() 存在极大值与极小值,求实数
存在极大值与极小值,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游爱好者计划从3个亚洲国家A1,A2,A3和3个欧洲国家B1,B2,B3中选择2个国家去旅游.
(1)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(2)若从亚洲国家和欧洲国家中各选1个,求这两个国家包括A1,但不包括B1的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】九十年代,政府间气候变化专业委员会(IPCC)提供的一项报告指出:使全球气候逐年变暖的一个重要因素是人类在能源利用与森林砍伐中使CO2浓度增加.据测,1990年、1991年、1992年大气中的CO2浓度分别比1989年增加了1个可比单位、3个可比单位、6个可比单位。若用函数模拟九十年代中每年CO2浓度增加的可比单位数y与年份增加数x的关系,模拟函数可选用二次函数或函数![]() (其中a、b、c为常数).
(其中a、b、c为常数).
(Ⅰ)写出这两个函数的解释式;
(Ⅱ)若知1994年大气中的CO2浓度比1989年增加了16个可比单位,请问用以上哪个函数作为模拟函数与1994年的实际数据更接近?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量![]() 单位:吨
单位:吨![]() ,将数据按照
,将数据按照![]() ,
,![]() ,
,![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
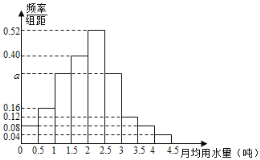
(1)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数![]() 说明理由;
说明理由;
(2)估计居民月均用水量的中位数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com