

分析 连结O′A′,OA,过A′作A′E⊥OA,交OA于点E,分别求出AE,A′E,由此能求出它的侧棱长.
解答 解:连结O′A′,OA,过A′作A′E⊥OA,交OA于点E,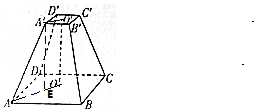
∵正四棱台的上底面边长为2,下底面边长为8,高为3$\sqrt{2}$,
∴AE=$\frac{1}{2}\sqrt{{8}^{2}+{8}^{2}}$-$\frac{1}{2}\sqrt{{2}^{2}+{2}^{2}}$=3$\sqrt{2}$,A′E=3$\sqrt{2}$,
∴它的侧棱长AA′=$\sqrt{(3\sqrt{2})^{2}+(3\sqrt{2})^{2}}$=6.
故答案为:6.
点评 本题考查正四棱台的侧棱长的求法,是基础题,解题时要认真审题,注意正四棱台的性质的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | (-2018,-2016) | B. | (-∞,-2016) | C. | (-2019,-2016) | D. | (-∞,-2019) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
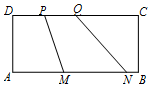 如图,矩形ABCD中,AB=2AD=4,MN=2PQ=2,向该矩形内随机投一质点,则质点落在四边形MNQP内的概率为( )
如图,矩形ABCD中,AB=2AD=4,MN=2PQ=2,向该矩形内随机投一质点,则质点落在四边形MNQP内的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{3}{8}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
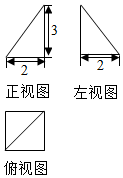 已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )
已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是( )| A. | $\frac{4}{3}$cm3 | B. | $\frac{8}{3}$cm3 | C. | 2cm3 | D. | 4cm3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
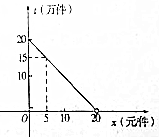 2016年9月,第22届鲁台经贸洽谈会在潍坊鲁台会展中心举行,在会展期间某展销商销售一种商品,根据市场调查,每件商品售价x(元)与销量t(万元)之间的函数关系如图所示,又知供货价格与销量呈反比,比例系数为20.(注:每件产品利润=售价-供货价格)
2016年9月,第22届鲁台经贸洽谈会在潍坊鲁台会展中心举行,在会展期间某展销商销售一种商品,根据市场调查,每件商品售价x(元)与销量t(万元)之间的函数关系如图所示,又知供货价格与销量呈反比,比例系数为20.(注:每件产品利润=售价-供货价格)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com