四川灾后重建工程督导评估小组五名专家被随机分配到A、B、C、D四所不同的学校进行重建评估工作,要求每所学校至少有一名专家.
(1)求评估小组中甲、乙两名专家同时被分配到A校的概率;
(2)求评估小组中甲、乙两名专家不在同一所学校的概率;
(3)设随机变量ξ为这五名专家到A校评估的人数,求ξ的数学期望Eξ.
分析:(1)由已知中五名专家被随机分配到A、B、C、D四所不同的学校,我们易计算出所有可能的分配方案和甲、乙两名专家同时被分配到A校的分配方案,代入古典概型公式,即可求出结果.
(2)类比(1)的处理办法,计算出所有可能的分配方案和甲、乙两名专家不在同一所学校,代入古典概型公式,即可求出结果.
(3)由于每所学校至少有一名专家,则随机变量ξ的可能取值为1,2,分类讨论随机变量ξ取1和2时的概率,列出ξ的分布列后,代入数学期望公式即可求出答案.
解答:解:(1)记评估小组中甲、乙两名专家同时被分配到A校的事件为E,则P(E)=
=,所以评估小组中甲、乙两名专家同时被分配到A校的概率为
.
(2)记评估小组中甲、乙两名专家被分配在同一所学校的事件为F,那么P(F)=
=,所以甲、乙两名专家不在同一所学校的概率为:P(
)=1-P(F)=
.
(3)随机变量ξ的可能取值为1,2,则P(ξ=2)=
=;P(ξ=1)=1-P(ξ=2)=
.
所以ξ的分布列是:
所以ξ的数学期望Eξ=1×
+2×
=
.
点评:本题考查的知识是等可能性事件的概率及离散型随机变量的期望与方差,利用排列组合公式求出基本事件的总数和满足某个事件的基本事件个数是解答本题的关键.



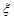 为这五名专家到A校评估的人数,求
为这五名专家到A校评估的人数,求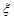 的数学期望E
的数学期望E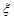 。
。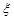 为这五名专家到A校评估的人数,求
为这五名专家到A校评估的人数,求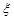 的数学期望E
的数学期望E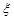 。
。