
【题目】已知一个正多边形的每条边和对角线恰各染成2018种颜色之一,且所有边及对角线不全同色.若正多边形中不存在两色三角形(即三角形的三边恰被染成两种颜色),则称该多边形的染色是“和谐的”.求最大的正整数![]() ,使得存在一个和谐的染色正
,使得存在一个和谐的染色正![]() 边形.
边形.
【答案】![]()
【解析】
先考虑和谐染色的正![]() 边形的任意一个顶点
边形的任意一个顶点![]() .可证明:对于每种颜色,由
.可证明:对于每种颜色,由![]() 至多可以引出2016条该种颜色的边.
至多可以引出2016条该种颜色的边.
否则,设![]() 与顶点
与顶点![]() 相连的边有相同的颜色(记为
相连的边有相同的颜色(记为![]() ),于是,
),于是,![]() 两两之间连边的颜色均为
两两之间连边的颜色均为![]() .
.
令顶点![]() 为与
为与![]() 相连的边异于颜色
相连的边异于颜色![]() 的一个顶点(此顶点必然存在,否则,正
的一个顶点(此顶点必然存在,否则,正![]() 边形的所有边均为颜色
边形的所有边均为颜色![]() ,与条件矛盾).此时,顶点
,与条件矛盾).此时,顶点![]() 与
与![]() 的连边两两不同色,且均不为颜色
的连边两两不同色,且均不为颜色![]() ,这样至少有2019种颜色,与条件矛盾.
,这样至少有2019种颜色,与条件矛盾.
从而,在和谐染色的正多边形中,任一顶点引出的边数为![]()
![]() .
.
再证明:存在和谐的染色正![]() 边形.
边形.
注意到,2017为素数.
故对任意整数 ![]() ,及任意整数
,及任意整数![]() ,均存在唯一的
,均存在唯一的![]() ,使得
,使得![]() .
.
用![]() 表示
表示![]() 个顶点,其中,
个顶点,其中,![]() 、
、![]() ,数字0,1,…,2017表示2018种颜色.
,数字0,1,…,2017表示2018种颜色.
对于顶点![]() 和
和![]() ,当
,当![]() 时,
时,
若![]() ,
,
则将![]() 与
与![]() 之间的连边染颜色
之间的连边染颜色![]() ;
;
若![]() ,则将
,则将![]() 与
与![]() 之间的连边染色颜色2017.
之间的连边染色颜色2017.
由2017为素数,知染色方式唯一确定.
下面证明:这样的染色方式是和谐的.
对于任意三个顶点![]() 、
、![]() 、
、![]() ,若
,若![]() 、
、![]() 与
与 ![]() 、
、![]() 之间的连边同色,则
之间的连边同色,则![]() 、
、![]() 之间的连边也必为此种颜色.
之间的连边也必为此种颜色.
事实上,若![]() 、
、![]() 与
与![]() 、
、![]() 之间的连边同为颜色2017,则
之间的连边同为颜色2017,则![]() .故
.故![]() 、
、![]() 之间的连边也为颜色2017.
之间的连边也为颜色2017.
若![]() 、
、![]() 与
与![]() 、
、![]() 之间的连边同为颜色
之间的连边同为颜色![]() ,
,
则![]() ,
,![]() .
.
故![]() .
.
从而,![]() 、
、![]() 之间的连边也为颜色
之间的连边也为颜色 ![]() .
.
综上,满足条件的![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}满足![]() an+1
an+1![]() an=0(n∈N*),且
an=0(n∈N*),且![]() ,
,![]() ,
,![]() 成等差数列.
成等差数列.
(1)求数列{an}的通项公式;
(2)令bn=![]() (n∈N*),求数列{bn}的前n项和为
(n∈N*),求数列{bn}的前n项和为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 在第一象限内的点
在第一象限内的点![]() 到焦点F的距离为
到焦点F的距离为![]() .
.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 与抛物线C相交于A,B两点,与圆
与抛物线C相交于A,B两点,与圆![]() 相交于D,E两点,O为坐标原点,
相交于D,E两点,O为坐标原点,![]() ,试问:是否存在实数a,使得|DE|的长为定值?若存在,求出a的值;若不存在,请说明理由.
,试问:是否存在实数a,使得|DE|的长为定值?若存在,求出a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某蔬果经销商销售某种蔬果,售价为每公斤25元,成本为每公斤15元.销售宗旨是当天进货当天销售.如果当天卖不出去,未售出的全部降价以每公斤10元处理完.根据以往的销售情况,得到如图所示的频率分布直方图:

(1)根据频率分布直方图计算该种蔬果日需求量的平均数![]() (同一组中的数据用该组区间中点值代表);
(同一组中的数据用该组区间中点值代表);
(2)该经销商某天购进了250公斤这种蔬果,假设当天的需求量为![]() 公斤
公斤![]() ,利润为
,利润为![]() 元.求
元.求![]() 关于
关于![]() 的函数关系式,并结合频率分布直方图估计利润
的函数关系式,并结合频率分布直方图估计利润![]() 不小于1750元的概率.
不小于1750元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() ,直线
,直线 ![]() .以极点
.以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的正半轴建立平面直角坐标系.
轴的正半轴建立平面直角坐标系.
(1)求直线![]() ,
,![]() 的直角坐标方程以及曲线
的直角坐标方程以及曲线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,直线
两点,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别是BC、CD的中点,G是EF的中点,现在沿AE、AF及EF把这个正方形折成一个空间图形,使B、C、D三点重合,重合后的点记为H,那么,在这个空间图形中必有( )
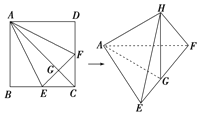
A. ![]() 所在平面B.
所在平面B. ![]() 所在平面
所在平面
C. ![]() 所在平面D.
所在平面D. ![]() 所在平面
所在平面
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章给出计算弧田面积所用的经验方式为:弧田面积=![]() ,弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”指半径长与圆心到弦的距离之差。现有圆心角为
,弧田(如图)由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”指半径长与圆心到弦的距离之差。现有圆心角为![]() ,半径等于4米的弧田.下列说法不正确的是( )
,半径等于4米的弧田.下列说法不正确的是( )

A. “弦”![]() 米,“矢”
米,“矢”![]() 米
米
B. 按照经验公式计算所得弧田面积(![]() )平方米
)平方米
C. 按照弓形的面积计算实际面积为(![]() )平方米
)平方米
D. 按照经验公式计算所得弧田面积比实际面积少算了大约0.9平方米(参考数据![]()
![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 的三条内线段
的三条内线段![]() 、
、![]() 、
、![]() 交于点
交于点![]() 、用红、蓝两种颜色对
、用红、蓝两种颜色对![]() 的三条边线和三条内线段染色,使同色的三线不交于一点.证明:在图中所有的三角形中,至少存在两个同色三角形,且它的各边或延长线被另一线截得的两线段之比的和大于3.
的三条边线和三条内线段染色,使同色的三线不交于一点.证明:在图中所有的三角形中,至少存在两个同色三角形,且它的各边或延长线被另一线截得的两线段之比的和大于3.
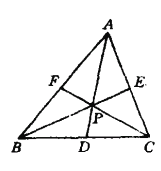
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com