
【题目】某厂为检验车间一生产线是否工作正常,现从生产线中随机抽取一批零件样本,测量尺寸(单位: mm )绘成频率分布直方图如图所示:
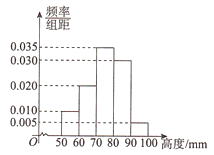
(Ⅰ)求该批零件样本尺寸的平均数 x 和样本方差 ![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)若该批零件尺寸![]() 服从正态分布
服从正态分布 ![]() ,其中
,其中 ![]() 近似为样本平均数
近似为样本平均数 ![]() 近似为样本方差
近似为样本方差 ![]() ,利用该正态分布求
,利用该正态分布求 ![]() ;
;
(Ⅲ)若从生产线中任取一零件,测量尺寸为30mm,根据 ![]() 原则判断该生产线是否正常?
原则判断该生产线是否正常?
附: ![]() ;若
;若![]() ,则
,则 ![]() ,
, ![]() ,
,![]() .
.
 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P﹣ABCD的底面为平行四边形,PD⊥平面ABCD,M为PC中点.
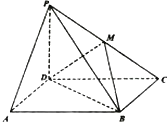
(1)求证:AP∥平面MBD;
(2)若AD⊥PB,求证:BD⊥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱柱BCF﹣ADE的侧面CFED与ABFE都是边长为1的正方形,M、N两点分别在AF和CE上,且AM=EN.
(1)求证:平面ABCD⊥平面ADE;
(2)求证:MN∥平面BCF;
(3)若点N为EC的中点,点P为EF上的动点,试求PA+PN的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在下列向量组中,可以把向量![]() =(3,2)表示出来的是( )
=(3,2)表示出来的是( )
A.![]() =(0,0),
=(0,0),![]() =(1,2)
=(1,2)
B.![]() =(﹣1,2),
=(﹣1,2),![]() =(5,﹣2)
=(5,﹣2)
C.![]() =(3,5),
=(3,5),![]() =(6,10)
=(6,10)
D.![]() =(2,﹣3),
=(2,﹣3), ![]() =(﹣2,3)
=(﹣2,3)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,点P(2,0).
,点P(2,0).
(I)求椭圆C的短轴长与离心率;
( II)过(1,0)的直线![]() 与椭圆C相交于M、N两点,设MN的中点为T,判断|TP|与|TM|的大小,并证明你的结论.
与椭圆C相交于M、N两点,设MN的中点为T,判断|TP|与|TM|的大小,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=1-![]() (a>0且a≠1)是定义在(-∞,+∞)上的奇函数.
(a>0且a≠1)是定义在(-∞,+∞)上的奇函数.
(1)求a的值;
(2)证明:函数f(x)在定义域(-∞,+∞)内是增函数;
(3)当x∈(0,1]时,tf(x)≥2x-2恒成立,求实数t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com