
【题目】如图,斜三棱柱![]() 中,
中,![]() 是边长为2的正三角形,
是边长为2的正三角形,![]() 为
为![]() 的中点,
的中点,![]() 平面
平面![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,
,![]() 为
为![]() 与
与![]() 的交点,且
的交点,且![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
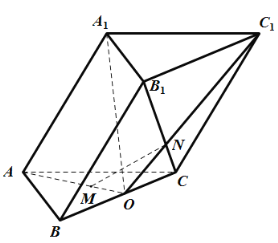
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)连结![]() ,证明相似得到
,证明相似得到![]() ,得到证明.
,得到证明.
(2)以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图所示的空间直角坐标系,平面
轴建立如图所示的空间直角坐标系,平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,计算夹角得到答案.
,计算夹角得到答案.
(1)连结![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.

(2)因为![]() 是边长为2的正三角形,
是边长为2的正三角形,![]() 为
为![]() 的中点,
的中点,![]() 平面
平面![]() ,
,
所以,![]() ,
,![]() ,
,![]() 两两垂直,以
两两垂直,以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立如图所示的空间直角坐标系.
轴建立如图所示的空间直角坐标系.
![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,又
,又![]() ∥
∥![]() ,
,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
又![]() 平面
平面![]() ,
,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,即
,即![]() .
.
又![]() 是边长为2的正三角形,
是边长为2的正三角形,![]() 为
为![]() 的中点,
的中点,![]() ,
,
由题意知,![]() ,
,![]() ,
,![]() ,
,
所以,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
所以, ,即
,即 ,取
,取![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
由 ,得
,得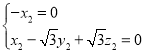 ,取
,取![]() ,
,
所以 ,
,
设二面角![]() 的大小为
的大小为![]() ,
,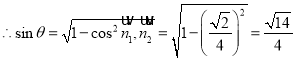 .
.
所以二面角![]() 的正弦值为
的正弦值为![]() .
.



科目:高中数学 来源: 题型:
【题目】某公司准备设计一个精美的心形巧克力盒子,它是由半圆![]() 、半圆
、半圆![]() 和正方形ABCD组成的,且
和正方形ABCD组成的,且![]() .设计人员想在心形盒子表面上设计一个矩形的标签EFGH,标签的其中两个顶点E,F在AM上,另外两个顶点G,H在CN上(M,N分别是AB,CB的中点).设EF的中点为P,
.设计人员想在心形盒子表面上设计一个矩形的标签EFGH,标签的其中两个顶点E,F在AM上,另外两个顶点G,H在CN上(M,N分别是AB,CB的中点).设EF的中点为P,![]() ,矩形EFGH的面积为
,矩形EFGH的面积为![]() .
.
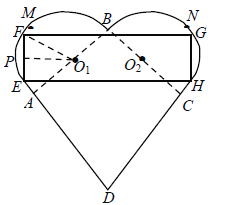
(1)写出S关于![]() 的函数关系式
的函数关系式![]()
(2)当![]() 为何值时矩形EFGH的面积最大?
为何值时矩形EFGH的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,斜三棱柱![]() 中,
中,![]() 是边长为2的正三角形,
是边长为2的正三角形,![]() 为
为![]() 的中点,
的中点,![]() 平面
平面![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,
,![]() 为
为![]() 与
与![]() 的交点,且
的交点,且![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
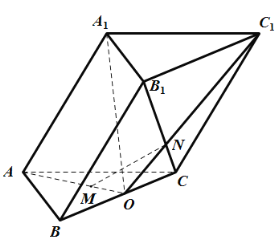
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图1是某高架桥箱梁的横截面,它由上部路面和下部支撑箱两部分组成.如图2,路面宽度![]() ,下部支撑箱CDEF为等腰梯形(
,下部支撑箱CDEF为等腰梯形(![]() ),且
),且![]() .为了保证承重能力与稳定性,需下部支撑箱的面积为
.为了保证承重能力与稳定性,需下部支撑箱的面积为![]() ,高度为2m且
,高度为2m且![]() ,若路面AB.侧边CF和DE,底部EF的造价分别为4a千元/m,5a千元/m,6a千元/m(a为正常数),
,若路面AB.侧边CF和DE,底部EF的造价分别为4a千元/m,5a千元/m,6a千元/m(a为正常数),![]() .
.

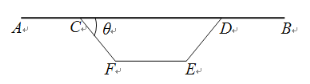
(1)试用θ表示箱梁的总造价y(千元);
(2)试确定cosθ的值,使总造价最低?并求最低总造价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】斜率为![]() 的直线
的直线![]() 过抛物线
过抛物线![]() :
:![]() 的焦点
的焦点![]() ,且与拋物线
,且与拋物线![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)设点![]() 在笫一象限,过
在笫一象限,过![]() 作拋物线
作拋物线![]() 的准线的垂线,
的准线的垂线,![]() 为垂足,且
为垂足,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)过![]() 且与
且与![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() :
:![]() 交于
交于![]() ,
,![]() 两点,若
两点,若![]() 与
与![]() 面积之和为
面积之和为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生物公司将A型病毒疫苗用100只小白鼠进行科研和临床试验,得到统计数据如表:
未感染病毒 | 感染病毒 | 总计 | |
未注射 | 10 | x | A |
注射 | 40 | y | B |
总计 | 50 | 50 | 100 |
现从所有试验的小白鼠中任取一只,取得注射疫苗小白鼠的概率为![]() .
.
(1)能否有99.9%的把握认为注射此型号疫苗有效?
(2)现从感染病毒的小白鼠中任取3只进行病理分析,记已注射疫苗的小白鼠只数为ξ,求ξ的分布列和数学期望.
附: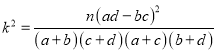
P(K2≥k0) | 0.10 | 0.010 | 0.001 |
k0 | 2.706 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com