
【题目】已知椭圆![]() 的右焦点为F,离心率为
的右焦点为F,离心率为![]() ,直线l:
,直线l:![]() 与椭圆E相交于A,B两点,
与椭圆E相交于A,B两点,![]() .
.
![]() 1
1![]() 求椭圆E的标准方程;
求椭圆E的标准方程;
![]() 2
2![]() 延长AF交椭圆E于点M,延长BF交椭圆E于点N,若直线MN的斜率为1,求实数m的值.
延长AF交椭圆E于点M,延长BF交椭圆E于点N,若直线MN的斜率为1,求实数m的值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱台![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,
,![]() ,
,![]() 平面
平面![]() .
.

(1)若点![]() 是
是![]() 的中点,求证:
的中点,求证:![]() //平面
//平面![]() ;
;
(2)棱BC上是否存在一点E,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求线段CE的长;若不存在,请说明理由.
?若存在,求线段CE的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系的原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,已知直线
轴的正半轴为极轴,建立极坐标系,已知直线![]() 的参数方程是
的参数方程是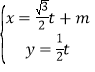 (m>0,t为参数),曲线
(m>0,t为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与曲线
,与曲线![]() 交于点
交于点![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某居民最近连续几年的月用水量进行统计,得到该居民月用水量![]() 单位:吨
单位:吨![]() 的频率分布直方图,如图一.
的频率分布直方图,如图一.

![]() 根据频率分布直方图估计该居民月平均用水量
根据频率分布直方图估计该居民月平均用水量![]() ;
;
![]() 已知该居民月用水量T与月平均气温
已知该居民月用水量T与月平均气温![]() 单位:
单位:![]() 的关系可用回归直线
的关系可用回归直线![]() 模拟
模拟![]() 年当地月平均气温t统计图如图二,把2017年该居民月用水量高于和低于
年当地月平均气温t统计图如图二,把2017年该居民月用水量高于和低于![]() 的月份分为两层,用分层抽样的方法选取5个月,再从这5个月中随机抽取2个月,这2个月中该居民有
的月份分为两层,用分层抽样的方法选取5个月,再从这5个月中随机抽取2个月,这2个月中该居民有![]() 个月每月用水量超过
个月每月用水量超过![]() ,视频率为概率,求出
,视频率为概率,求出![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现将甲、乙两个学生在高二的6次数学测试的成绩(百分制)制成如图所示的茎叶图,进入高三后,由于改进了学习方法,甲、乙这两个学生的考试成绩预计同时有了大的提升:若甲(乙)的高二任意一次考试成绩为![]() ,则甲(乙)的高三对应的考试成绩预计为
,则甲(乙)的高三对应的考试成绩预计为![]() .
.

(1)试预测:高三6次测试后,甲、乙两个学生的平均成绩分别为多少?谁的成绩更稳定?
(2)若已知甲、乙两个学生的高二6次考试成绩分别由低到高进步的,定义![]() 为高三的任意一次考试后甲、乙两个学生的当次成绩之差的绝对值,求
为高三的任意一次考试后甲、乙两个学生的当次成绩之差的绝对值,求![]() 的平均值.
的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年是中国传统的农历“鼠年”,有人用3个圆构成“卡通鼠”的形象,如图:![]() 是圆Q的圆心,圆Q过坐标原点O;点L、S均在x轴上,圆L与圆S的半径都等于2,圆S、圆L均与圆Q外切.已知直线l过点O.
是圆Q的圆心,圆Q过坐标原点O;点L、S均在x轴上,圆L与圆S的半径都等于2,圆S、圆L均与圆Q外切.已知直线l过点O.
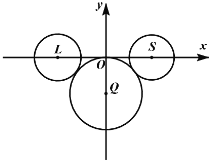
(1)若直线l与圆L、圆S均相切,则l截圆Q所得弦长为__________;
(2)若直线l截圆L、圆S、圆Q所得弦长均等于d,则![]() __________.
__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com