分析:(1)根据题意,以DA、DC、DD
1所在直线分别为x、y、z轴,建立如图所示空间直角坐标系.可得
、
的坐标,从而算出
•
=0,由此即可得到AF和BE所成的角为90°.
(2)根据AA
1∥BB
1,可得BB
1与平面BEC
1所成角等于AA
1与平面BEC
1所成角.由
VB1-BEC1=
VB-B1EC1利用等体积转换,代入题中数据算出B
1到平面BEC
1的距离等于1,再根据直线与平面所成角的定义与性质,可得AA
1与平面BEC
1所成角的大小.
解答:解:
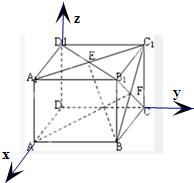
(1)以DA、DC、DD
1所在直线分别为x、y、z轴,
建立如图所示空间直角坐标系,可得
A(2,0,0),B(2,2,0),E(1,1,
),F(1,2,
)
∴
=(-1,2,
),
=(-1,-1,
)
可得
•
=-1×(-1)+2×(-1)+
×
=0
因此
⊥
,即AF和BE所成的角为90°;
(2)∵长方体AC中,AA
1∥BB
1,
∴BB
1与平面BEC
1所成角等于AA
1与平面BEC
1所成角.
设点B
1到平面BEC
1的距离等于d,则
V
B1-BEC1=V
B-B1EC1,即
S
△BEC1×d=
S
△B1EC1 ×BB
1∵BE=
=
=
=2,EC
1=
A
1C
1=
,∠BEC
1=90°
∴S
△BEC1=
BE×EC
1=
∵S
△B1EC1 =
SA1 B1C1D1=1,
∴
×
×d=
×1×
,解之得d=1.
设BB
1与平面BEC
1所成角为α,则sinα=
=
,得α=45°,
∴BB
1与平面BEC
1所成角为45°,即AA
1与平面BEC
1所成角等于45°.
点评:本题在长方体中求异面直线所成角的大小和直线与平面所成角的大小,着重考查了长方体的性质和利用空间向量研究异面直线所成角、直线与平面所成角的定义与求法等知识,属于中档题.

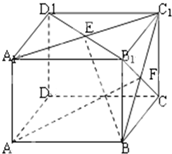 如图,在长方体AC中,AB=BC=2,AA1=
如图,在长方体AC中,AB=BC=2,AA1= (1)以DA、DC、DD1所在直线分别为x、y、z轴,
(1)以DA、DC、DD1所在直线分别为x、y、z轴,

 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案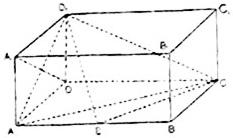 如图,在长方体ABCD-A1B1C1D1中,AD=AA1,AB=2,点E在棱AB上.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1,AB=2,点E在棱AB上.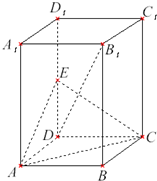 如图,在长方体ABCD-A1B1C1D1中,底面ABCD是正方形,E是DD1的中点.
如图,在长方体ABCD-A1B1C1D1中,底面ABCD是正方形,E是DD1的中点.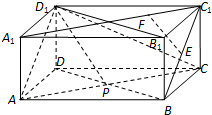 如图,在长方体ABCD-A1B1C1D1中,AB=AD=2.
如图,在长方体ABCD-A1B1C1D1中,AB=AD=2.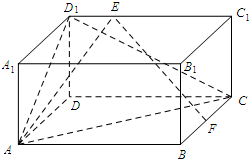 如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=2,A1A=2,点F是棱BC的中点,点E在棱C1D1上,且D1E=λEC1(λ为实数).
如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=2,A1A=2,点F是棱BC的中点,点E在棱C1D1上,且D1E=λEC1(λ为实数).