
【题目】已知椭圆G: ![]() 的两个焦点分别为F1和F2 , 短轴的两个端点分别为B1和B2 , 点P在椭圆G上,且满足|PB1|+|PB2|=|PF1|+|PF2|.当b变化时,给出下列三个命题: ①点P的轨迹关于y轴对称;
的两个焦点分别为F1和F2 , 短轴的两个端点分别为B1和B2 , 点P在椭圆G上,且满足|PB1|+|PB2|=|PF1|+|PF2|.当b变化时,给出下列三个命题: ①点P的轨迹关于y轴对称;
②存在b使得椭圆G上满足条件的点P仅有两个;
③|OP|的最小值为2,
其中,所有正确命题的序号是 .
【答案】①③
【解析】解:椭圆G: ![]() 的两个焦点分别为
的两个焦点分别为
F1( ![]() ,0)和F2(﹣
,0)和F2(﹣ ![]() ,0),
,0),
短轴的两个端点分别为B1(0,﹣b)和B2(0,b),
设P(x,y),点P在椭圆G上,且满足|PB1|+|PB2|=|PF1|+|PF2|,
由椭圆定义可得,|PB1|+|PB2|=2a=2 ![]() >2b,
>2b,
即有P在椭圆 ![]() +
+ ![]() =1上.
=1上.
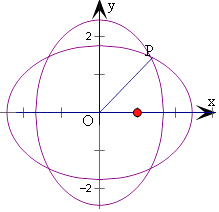
对于①,将x换为﹣x方程不变,则点P的轨迹关于y轴对称,
故①正确;
对于②,由图象可得轨迹关于x,y轴对称,且0<b< ![]() ,
,
则椭圆G上满足条件的点P有4个,
不存在b使得椭圆G上满足条件的点P仅有两个,故②不正确;
对于③,由图象可得,当P满足x2=y2,即有6﹣b2=b2,即b= ![]() 时,
时,
|OP|取得最小值,可得x2=y2=2,即有|OP|的最小值为2,故③正确.
所以答案是:①③.


科目:高中数学 来源: 题型:
【题目】据统计,某物流公司每天的业务中,从甲地到乙地的可配送的货物量X(40≤X<200,单位:件)的频率分布直方图,如图所示,将频率视为概率,回答以下问题. 
(1)求该物流公司每天从甲地到乙地平均可配送的货物量;
(2)该物流公司拟购置货车专门运营从甲地到乙地的货物,一辆货车每天只能运营一趟,每辆车每 趟最多只能装载40 件货物,满载发车,否则不发车.若发车,则每辆车每趟可获利1000 元;若未发车,
则每辆车每天平均亏损200 元.为使该物流公司此项业务的营业利润最大,该物流公司应该购置几辆货
车?
查看答案和解析>>
科目:高中数学 来源: 题型:
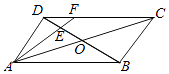
【题目】在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD相交于点F.若AB=2, ![]() ,∠BAD=45°,则
,∠BAD=45°,则 ![]() =( )
=( )
A.![]()
B.1
C.﹣ ![]()
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:函数f(x)=x3+ax2+x在R上是增函数;命题q:若函数g(x)=ex﹣x+a在区间[0,+∞)没有零点.
(1)如果命题p为真命题,求实数a的取值范围;
(2)命题“p∨q”为真命题,“p∧q”为假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将集合M={1,2,3,…15}表示为它的5个三元子集(三元集:含三个元素的集合)的并集,并且这些三元子集的元素之和都相等,则每个三元集的元素之和为;请写出满足上述条件的集合M的5个三元子集 . (只写出一组)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于无穷数列{an},记T={x|x=aj﹣ai , i<j},若数列{an}满足:“存在t∈T,使得只要am﹣ak=t(m,k∈N*且m>k),必有am+1﹣ak+1=t”,则称数列{an}具有性质P(t). (Ⅰ)若数列{an}满足 ![]() 判断数列{an}是否具有性质P(2)?是否具有性质P(4)?
判断数列{an}是否具有性质P(2)?是否具有性质P(4)?
(Ⅱ)求证:“T是有限集”是“数列{an}具有性质P(0)”的必要不充分条件;
(Ⅲ)已知{an}是各项为正整数的数列,且{an}既具有性质P(2),又具有性质P(5),求证:存在整数N,使得aN , aN+1 , aN+2 , …,aN+k , …是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为研究学生语言学科的学习情况,现对高二200名学生英语和语文某次考试成绩进行抽样分析.将200名学生编号为001,002,…,200,采用系统抽样的方法等距抽取10名学生,将10名学生的两科成绩(单位:分)绘成折线图如下: 
(Ⅰ)若第一段抽取的学生编号是006,写出第五段抽取的学生编号;
(Ⅱ)在这两科成绩差超过20分的学生中随机抽取2人进行访谈,求2人成绩均是语文成绩高于英语成绩的概率;
(Ⅲ)根据折线图,比较该校高二年级学生的语文和英语两科成绩,写出你的结论和理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正△ABC三个顶点都在半径为2的球面上,球心O到平面ABC的距离为1,点E是线段AB的中点,过点E作球O的截面,则截面面积的最小值是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥中P﹣ABCD,底面ABCD为边长为 ![]() 的正方形,PA⊥BD.
的正方形,PA⊥BD.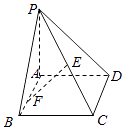
(1)求证:PB=PD;
(2)若E,F分别为PC,AB的中点,EF⊥平面PCD,求直线PB与平面PCD所成角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com