
【题目】若数列{an}是公差为2的等差数列,数列{bn}满足b1=1,b2=2,且anbn+bn=nbn+1.
(1)求数列{an},{bn}的通项公式;
(2)设数列{cn}满足![]() ,数列{cn}的前n项和为Tn,若不等式(-1)nλ<Tn+
,数列{cn}的前n项和为Tn,若不等式(-1)nλ<Tn+![]() 对一切n∈N*恒成立,求实数λ的取值范围.
对一切n∈N*恒成立,求实数λ的取值范围.
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人独立地对某一技术难题进行攻关。甲能攻克的概率为![]() ,乙能攻克的概率为
,乙能攻克的概率为![]() ,丙能攻克的概率为
,丙能攻克的概率为![]() .
.
(1)求这一技术难题被攻克的概率;
(2)若该技术难题末被攻克,上级不做任何奖励;若该技术难题被攻克,上级会奖励![]() 万元。奖励规则如下:若只有1人攻克,则此人获得全部奖金
万元。奖励规则如下:若只有1人攻克,则此人获得全部奖金![]() 万元;若只有2人攻克,则奖金奖给此二人,每人各得
万元;若只有2人攻克,则奖金奖给此二人,每人各得![]() 万元;若三人均攻克,则奖金奖给此三人,每人各得
万元;若三人均攻克,则奖金奖给此三人,每人各得![]() 万元。设甲得到的奖金数为X,求X的分布列和数学期望。(本题满分12分)
万元。设甲得到的奖金数为X,求X的分布列和数学期望。(本题满分12分)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位同学参加数学应用知识竞赛培训,现分别从他们在培训期间参加的若干次测试成绩中随机抽取8次,记录如下:
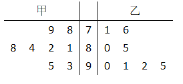
(Ⅰ)分别估计甲、乙两名同学在培训期间所有测试成绩的平均分;
(Ⅱ)从上图中甲、乙两名同学高于85分的成绩中各选一个成绩作为参考,求甲、乙两人成绩都在90分以上的概率;
(Ⅲ)现要从甲、乙中选派一人参加正式比赛,根据所抽取的两组数据分析,你认为选派哪位同学参加较为合适?说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设圆![]() 的圆心为A,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.
的圆心为A,直线l过点B(1,0)且与x轴不重合,l交圆A于C,D两点,过B作AC的平行线交AD于点E.
(I)证明![]() 为定值,并写出点E的轨迹方程;
为定值,并写出点E的轨迹方程;
(II)设点E的轨迹为曲线C1,直线l交C1于M,N两点,过B且与l垂直的直线与圆A交于P,Q两点,求四边形MPNQ面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数![]() ,试判断
,试判断![]() 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)若![]() 是定义在区间
是定义在区间![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 为定义域
为定义域![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com