
某同学在研究性学习中,收集到某制药厂车间工人数(单位:十人)与药品产量(单位:万盒)的数据如表所示:
| 工人数:x(单位:十人) | 1 | 2 | 3 | 4 |
| 药品产量:y(单位:万盒) | 3 | 4 | 5 | 6 |
 x+
x+ ;(参考数据
;(参考数据 i2=30,
i2=30,
 =50)
=50)科目:高中数学 来源: 题型:解答题
某班主任对班级22名学生进行了作业量多少的调查,数据如下表:在喜欢玩电脑游戏的12中,有10人认为作业多,2人认为作业不多;在不喜欢玩电脑游戏的10人中,有3人认为作业多,7人认为作业不多。求:(1)根据以上数据建立一个 列联表;(2)试问喜欢电脑游戏与认为作业多少是否有关系?
列联表;(2)试问喜欢电脑游戏与认为作业多少是否有关系?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
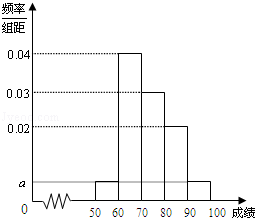
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求图中 的值;
的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数.
| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x:y | 1:1 | 2:1 | 3:4 | 4:5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某高校共有15000人,其中男生10500人,女生4500人,为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集300位学生每周平均体育运动时间的样本数据(单位:小时)
(1)应收集多少位女生样本数据?
(2)根据这300个样本数据,得到学生每周平均体育运动时间的频率分布直方图(如图所示),其中样本数据分组区间为: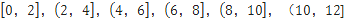 .估计该校学生每周平均体育运动时间超过4个小时的概率.
.估计该校学生每周平均体育运动时间超过4个小时的概率.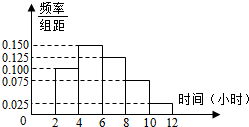
(3)在样本数据中,有60位女生的每周平均体育运动时间超过4个小时.请完成每周平均体育运动时间与性别的列联表,并判断是否有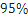 的把握认为“该校学生的每周平均体育运动时间与性别有关”.
的把握认为“该校学生的每周平均体育运动时间与性别有关”.
| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
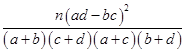
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某大学生在开学季准备销售一种文具套盒进行试创业,在一个开学季内,每售出1盒该产品获利润50元,未售出的产品,每盒亏损30元.根据历史资料,得到开学季市场需求量的频率分布直方图,如下图所示.该同学为这个开学季购进了160盒该产品,以X(单位:盒,100≤X≤200)表示这个开学季内的市场需求量,Y(单位:元)表示这个开学季内经销该产品的利润.
(1)根据直方图估计这个开学季内市场需求量X的平均数和众数;
(2)将Y表示为X的函数;
(3)根据直方图估计利润不少于4800元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
随机抽取某中学甲班10名同学,他们的身高(单位:cm)数据是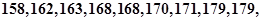
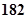 ;乙班10名同学,他们的身高(单位:cm)数据是
;乙班10名同学,他们的身高(单位:cm)数据是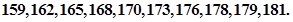
(1)画出甲、乙两班的茎叶图,并说明茎叶图有什么优点和缺点?
(2)根据茎叶图判断哪个班的平均身高较高(不必计算).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;
(2)求频率分布直方图中的a,b的值;
(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生该周课外阅读时间的平均数在第几组(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
今年一轮又一轮的寒潮席卷全国.某商场为了了解某品牌羽绒服的月销售量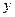 (件)与月平均气温
(件)与月平均气温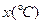 之间的关系,随机统计了某4个月的月销售量与当月平均气温,数据如下表:
之间的关系,随机统计了某4个月的月销售量与当月平均气温,数据如下表:
月平均气温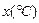 | 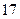 |  | 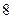 | 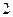 |
月销售量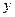 (件) (件) |  | 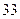 |  |  |
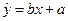 中的
中的 .气象部门预测下个月的平均气温约为
.气象部门预测下个月的平均气温约为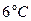 ,据此估计,
,据此估计,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com