
����Ŀ�����������⣺ ��y=|sinx�� ![]() |�������ǦУ�
|�������ǦУ�
��y=sinx+sin|x|��ֵ����[0��2]��
�۷���cosx=lgx�����⣻
�ܦ�Ϊ��ʵ����y=2sin��x�� ![]() �ϵ�������ô�ص�ȡֵ��Χ��
�ϵ�������ô�ص�ȡֵ��Χ�� ![]() ��
��
����y=3sin��2x+ ![]() ���У���f��x1��=f��x2��=0����x1��x2��Ϊ�е���������
���У���f��x1��=f��x2��=0����x1��x2��Ϊ�е���������
����A��B����ǡ�ABC�������ڽǣ����P��cosB��sinA��sinB��cosA�ڵڶ����ޣ�
���ڡ�ABC�У��� ![]() �����ABC�۽������Σ��������������Ϊ�� ��
�����ABC�۽������Σ��������������Ϊ�� ��
A.2
B.3
C.4
D.5
���𰸡�C
���������⣺���ڢ٣���y=|sin����x�� ![]() |��������
|�������� ![]() ������ȷ�� ���ڢڣ���x��0ʱ��y=sinx+sin|x|=2sinxֵ����[0��2]���ʴ���
������ȷ�� ���ڢڣ���x��0ʱ��y=sinx+sin|x|=2sinxֵ����[0��2]���ʴ���
���ڢۣ���lg2�У�1��lg4�У�1������cosx=lgx�����⣬��ȷ��
���ڢܣ���Ϊ��ʵ����y=2sin��x�� ![]() �ϵ������������������Һ����ĵ����Կɵæ�
�ϵ������������������Һ����ĵ����Կɵæ� ![]() �ܣ��ɴ���������صķ�Χ��
�ܣ��ɴ���������صķ�Χ�� ![]() ������ȷ��
������ȷ��
���ڢݣ�����������T=�У�����ֵ����0��x֮�����СֵΪ ![]() ������x1��x2����
������x1��x2���� ![]() �����������ʴ���
�����������ʴ���
���ڢޣ���A��B����ǡ�ABC�������ڽǣ� ![]() B��
B�� ![]() ��A���� cosB��sinA��0��sinB��cosA��0������ȷ��
��A���� cosB��sinA��0��sinB��cosA��0������ȷ��
��ѡ��C��
�����㾫����������Ҫ���������������ж���Ӧ�õ����֪ʶ�㣬��Ҫ�����������⻥Ϊ������⣬��������ͬ������ԣ���������Ϊ������������⣬���ǵ������û�й�ϵ������ȷ�����⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������ѡ�ֲμӸ��ִ���ʱ��5����ί��ķ����þ�Ҷͼ��ʾ����ͼ����s1��s2�ֱ��ʾ�ס���ѡ�ַ����ı����s1��s2�Ĺ�ϵ�ǣ� �� 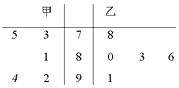
A.s1��s2
B.s1=s2
C.s1��s2
D.��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��tan����+ ![]() ��=��
��=�� ![]() ����
���� ![]() ����������
����������
��1����tan����ֵ��
��2���� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����dz����㣺 ![]() ��
��![]() ��������
��������![]() ��
Ϊ��![]() �������С�.
��������.
��1����![]() �ǡ�
�ǡ�![]() �������С���
����������![]() .��
.�� ![]() ��
��![]() ��ֵ��
��ֵ��
��2����![]() �ǡ�
�ǡ�![]() �������С�������
��������������![]() ��
�� ![]() ����
����![]() ����Сֵ��
����Сֵ��
��3����![]() �ǡ�0�������С���
�ǡ�0�������С���![]() ��������
��������![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() .֤����
.֤���� ![]() ��
��![]() ��.
��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijͬѧ�á���㷨�������� ![]() ������[��
������[�� ![]() ��
�� ![]() ]�ϵ�ͼ��ʱ���б��������˲������ݣ������
]�ϵ�ͼ��ʱ���б��������˲������ݣ������
2x�� | �� | ���� | �� | 0 |
|
|
x | �� | �� | �� |
|
|
|
f��x�� |
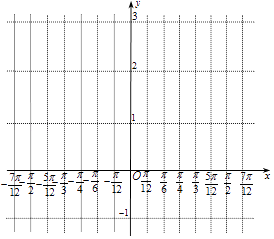
��1���뽫�ϱ����ݲ������������ڸ�����ֱ������ϵ�У�����f��x��������[�� ![]() ��
�� ![]() ]�ϵ�ͼ��
]�ϵ�ͼ��
��2����f��x������Сֵ��ȡ��Сֵʱx�ļ��ϣ�
��3����f��x���� ![]() ʱ��ֵ��
ʱ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ���Բ�οյأ������̼ƻ���һ��������Ӿ��![]() ������θ�����ʩ
������θ�����ʩ![]() ������ʣ��յؽ����̻����־�Ҫ���̻����Ӧ������а�Բ��Բ��Ϊ
������ʣ��յؽ����̻����־�Ҫ���̻����Ӧ������а�Բ��Բ��Ϊ![]() ���뾶Ϊ
���뾶Ϊ![]() �����ε�һ��
�����ε�һ��![]() ��ֱ���ϣ���
��ֱ���ϣ���![]() ��
��![]() ��
��![]() ��
��![]() ��Բ���ϣ�
��Բ���ϣ�![]() ��
��![]() �ڱ�
�ڱ�![]() �ϣ���
�ϣ���![]() ����
����![]() ��
��
��1������Ӿ�ؼ��丽����ʩ��ռ�����Ϊ![]() ����
����![]() �ı���ʽ��
�ı���ʽ��
��2��������Ʋ��ܷ����־ֵ�Ҫ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����A={x|1��x��3}������B={x|2m��x��1��m}��
��1����m=��1��A��B��
��2����A��B=����ʵ��m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
�� ![]() ��������Ϊ
��������Ϊ![]() ������Բ���������ĸ��˵�Ϊ����Ϊ�ı��ε����Ϊ
������Բ���������ĸ��˵�Ϊ����Ϊ�ı��ε����Ϊ![]() .
.
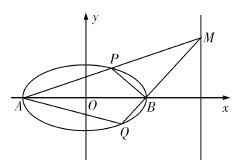
��������Բ![]() �ķ��̣�
�ķ��̣�
������ͼ��ʾ������Բ�����Ҷ���ֱ�Ϊ![]() ��
��![]() ��������
��������![]() �ڶ�ֱ��
�ڶ�ֱ��![]() ���˶�ʱ��ֱ��
���˶�ʱ��ֱ��![]() �ֱ���Բ������
�ֱ���Բ������![]() ��
��![]() �����ı���
�����ı���![]() ��������ֵ.
��������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������Ҫ����һ����������Ӿ�أ����ݻ�Ϊ4800m3 �� ��Ϊ3m���������رڵĵ���Ϊa�ҽ���صĵ����ǽ���رڵ�1.5�����������ˮ�صij��Ϳ�������ʹ�������ף��������Ƕ��٣�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com