
 ����O��AB���е㣬��P��AB���ӳ���
����O��AB���е㣬��P��AB���ӳ��� �ϣ���BP=3��һ����E��O���������ÿ��1����λ���ȵ��ٶ���OA�����˶�������A���������ԭ�ٶ���AO���أ���һ����F��P��
�ϣ���BP=3��һ����E��O���������ÿ��1����λ���ȵ��ٶ���OA�����˶�������A���������ԭ�ٶ���AO���أ���һ����F��P�� ��������ÿ��1����λ���ȵ��ٶ�������PA�����˶�����E��Fͬʱ����������������ʱֹͣ�˶����ڵ�E��F���˶������У���EFΪ�����ȱߡ�EFG��ʹ��EFG�;���ABCD������PA��ͬ�࣮���˶���ʱ��Ϊt�루t��0����
��������ÿ��1����λ���ȵ��ٶ�������PA�����˶�����E��Fͬʱ����������������ʱֹͣ�˶����ڵ�E��F���˶������У���EFΪ�����ȱߡ�EFG��ʹ��EFG�;���ABCD������PA��ͬ�࣮���˶���ʱ��Ϊt�루t��0���� ΪS�����S��t֮��ĺ�����ϵʽ����Ӧ���Ա���t��ȡֵ��Χ��
ΪS�����S��t֮��ĺ�����ϵʽ����Ӧ���Ա���t��ȡֵ��Χ��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ��x2��2x��5��x��[t��t��1]����f(x)����СֵΪh(t)��д��h(t)�ı���ʽ��
��x2��2x��5��x��[t��t��1]����f(x)����СֵΪh(t)��д��h(t)�ı���ʽ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
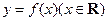 ��ͼ����㣨0��-3������
��ͼ����㣨0��-3������ �Ľ⼯
�Ľ⼯ .
. �Ľ���ʽ��
�Ľ���ʽ�� ����ֵ.
����ֵ.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
 ��ͼ����Կ����ɺ���
��ͼ����Կ����ɺ��� ��ͼ�������е�ƽ�Ƶõ� �� ��
��ͼ�������е�ƽ�Ƶõ� �� ��| A������ƽ��6��������ƽ��8 | B������ƽ��6��������ƽ��8 |
| C������ƽ��6��������ƽ��8 | D������ƽ��6��������ƽ��8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
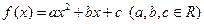 ��������������
��������������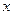 ��Rʱ��
��Rʱ��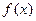 ����СֵΪ0����f (
����СֵΪ0����f (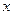 ��1)=f(��
��1)=f(��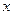 ��1)������
��1)������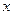 ��(0,5)ʱ��
��(0,5)ʱ��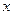 ��
��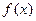 ��2
��2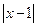 +1�������
+1�������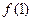 ��ֵ��
��ֵ�� 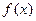 �Ľ���ʽ��
�Ľ���ʽ��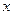 ��
��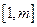 ʱ������
ʱ������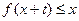 ������
�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
 ��
��| A���٢� | B���ۢ� | C���٢� | D���ڢ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 Ԫ�����۳�x��������Ʒʱ��ÿ���ļ۸�ΪpԪ������
Ԫ�����۳�x��������Ʒʱ��ÿ���ļ۸�ΪpԪ������ (a��b�dz���)��
(a��b�dz���)���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 �Ķ�����Ϊ[0 ��m],ֵ��Ϊ
�Ķ�����Ϊ[0 ��m],ֵ��Ϊ ���� m��ȡֵ��Χ��______________
���� m��ȡֵ��Χ��______________�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com