在平面直角坐标系xOy中,已知双曲线C1:2x2-y2=1.
(1)过C1的左顶点引C1的一条渐进线的平行线,求该直线与另一条渐进线及x轴围成的三角形的面积;
(2)设斜率为1的直线l交C1于P、Q两点,若l与圆x2+y2=1相切,求证:OP⊥OQ;
(3)设椭圆C2:4x2+y2=1,若M、N分别是C1、C2上的动点,且OM⊥ON,求证:O到直线MN的距离是定值.
【答案】
分析:(1)求出双曲线的渐近线方程,求出直线与另一条渐进线的交点,然后求出三角形的面积.
(2)设直线PQ的方程为y=kx+b,通过直线PQ与已知圆相切,得到b
2=2,通过求解

=0.证明PO⊥OQ.
(3)当直线ON垂直x轴时,直接求出O到直线MN的距离为

.当直线ON不垂直x轴时,设直线ON的方程为:y=kx,(显然|k|>

),推出直线OM的方程为y=

,利用

,求出

,

,设O到直线MN的距离为d,通过(|OM|
2+|ON|
2)d
2=|OM|
2|ON|
2,求出d=

.推出O到直线MN的距离是定值.
解答:解:(1)双曲线C
1:

左顶点A(-

),
渐近线方程为:y=±

x.
过A与渐近线y=

x平行的直线方程为y=

(x+

),即y=

,
所以

,解得

.
所以所求三角形的面积为S=

.
(2)设直线PQ的方程为y=kx+b,
因直线PQ与已知圆相切,故

,
即b
2=2,由

,
得x
2-2bx-b
2-1=0,
设P(x
1,y
1),Q(x
2,y
2),则

,
又y
1y
2=(x
1+b)(x
2+b).
所以

=x
1x
2+y
1y
2=2x
1x
2+b(x
1+x
2)+b
2
=2(-1-b
2)+2b
2+b
2
=b
2-2=0.
故PO⊥OQ.
(3)当直线ON垂直x轴时,|ON|=1,|OM|=

,则O到直线MN的距离为

.
当直线ON不垂直x轴时,设直线ON的方程为:y=kx,(显然|k|>

),
则直线OM的方程为y=

,由

得

,
所以

.
同理

,
设O到直线MN的距离为d,
因为(|OM|
2+|ON|
2)d
2=|OM|
2|ON|
2,
所以

=

=3,
即d=

.
综上,O到直线MN的距离是定值.
点评:本题考查直线与圆锥曲线的综合问题,圆锥曲线的综合,向量的数量积的应用,设而不求的解题方法,点到直线的距离的应用,考查分析问题解决问题的能力,考查计算能力.

 =0.证明PO⊥OQ.
=0.证明PO⊥OQ. .当直线ON不垂直x轴时,设直线ON的方程为:y=kx,(显然|k|>
.当直线ON不垂直x轴时,设直线ON的方程为:y=kx,(显然|k|> ),推出直线OM的方程为y=
),推出直线OM的方程为y= ,利用
,利用 ,求出
,求出 ,
, ,设O到直线MN的距离为d,通过(|OM|2+|ON|2)d2=|OM|2|ON|2,求出d=
,设O到直线MN的距离为d,通过(|OM|2+|ON|2)d2=|OM|2|ON|2,求出d= .推出O到直线MN的距离是定值.
.推出O到直线MN的距离是定值. 左顶点A(-
左顶点A(- ),
), x.
x. x平行的直线方程为y=
x平行的直线方程为y= (x+
(x+ ),即y=
),即y= ,
, ,解得
,解得 .
. .
. ,
, ,
, ,
, =x1x2+y1y2=2x1x2+b(x1+x2)+b2
=x1x2+y1y2=2x1x2+b(x1+x2)+b2 ,则O到直线MN的距离为
,则O到直线MN的距离为 .
. ),
), ,由
,由 得
得 ,
, .
. ,
, =
= =3,
=3, .
.

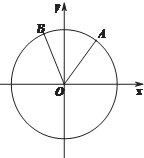 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是