
【题目】大庆实验中学在高二年级举办线上数学知识竞赛,在已报名的400名学生中,根据文理学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图:
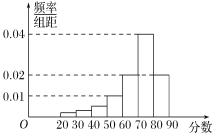
(1)估算一下本次参加考试的同学成绩的中位数和众数;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(3)已知样本中有一半理科生的分数不小于70,且样本中分数不小于70的文理科生人数相等.试估计总体中理科生和文科生人数的比例.
【答案】(1)中位数为72.5,众数为75(2)20(3)3∶2
【解析】
(1)算出每组的概率,进而找到50%落在哪个组,代入计算即可求解中位数,众数很明显在最高出中间位置产生;(2)先算出总体多少人再乘以[40,50)的概率即可求解;(3)先算出总共分数不小于70的人数, 从而算出样本中分数不小于70的理科生人数,再得到文科生人数即可求解。
解析:(1)可以估计出中位数为72.5,众数为75.
(2)根据题意,样本中分数不小于50的频率为(0.01+0.02+0.04+0.02)×10=0.9,
分数在区间[40,50)内的人数为100-100×0.9-5=5.
所以总体中分数在区间[40,50)内的人数估计为400×![]() =20.
=20.
(3)由题意可知,样本中分数不小于70的学生人数为(0.02+0.04)×10×100=60,
所以样本中分数不小于70的理科生人数为60×![]() =30.所以样本中的理科生人数为30×2=60,文科生人数为100-60=40,
=30.所以样本中的理科生人数为30×2=60,文科生人数为100-60=40,
所以根据分层抽样原理,总体中理科生和文科生人数的比例估计为60∶40=3∶2.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
【题目】如图,在正三棱柱 ABC﹣A1B1C1 中,AB 1 ,若二面角 C AB C1 的大小为 60°,则点 C 到平面 ABC1 的距离为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(12分)已知函数![]() .
.
(1)若x=2是函数f(x)的极值点,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若函数f(x)在![]() 上为单调增函数,求a的取值范围;
上为单调增函数,求a的取值范围;
(3)设m,n为正实数,且m>n,求证: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】居民消费价格指数(Consumer Price Index,简称![]() ),是度量居民生活消费品和服务价格水平随着时间变动的相对数,综合反映居民购买的生活消费品和服务价格水平的变动情况.如图为国家统计局于2020年4月公布的2019年3月至2020年3月
),是度量居民生活消费品和服务价格水平随着时间变动的相对数,综合反映居民购买的生活消费品和服务价格水平的变动情况.如图为国家统计局于2020年4月公布的2019年3月至2020年3月![]() 数据同比和环比涨跌幅折线图:
数据同比和环比涨跌幅折线图:
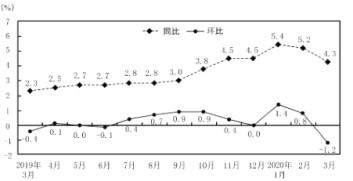
(注:同比![]() ,同比涨跌幅
,同比涨跌幅![]() ,环比
,环比![]() ,环比涨跌幅
,环比涨跌幅![]() ),则下列说法正确的是( )
),则下列说法正确的是( )
A.2019年12月与2018年12月![]() 相等
相等
B.2020年3月比2019年3月![]() 上涨4.3%
上涨4.3%
C.2019年7月至2019年11月![]() 持续增长
持续增长
D.2020年1月至2020年3月![]() 持续下降
持续下降
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 中,侧面
中,侧面![]() 底面
底面![]() ,
,![]() 是边长为2的正三角形,已知
是边长为2的正三角形,已知![]() 点满足
点满足![]() .
.
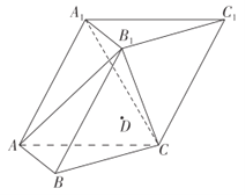
(1)求二面角![]() 的大小;
的大小;
(2)求异面直线![]() 与
与![]() 的距离;
的距离;
(3)直线![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面?若存在,请确定点
平面?若存在,请确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.命题“![]() ”的否定是“
”的否定是“![]() ”
”
B.命题“已知![]() ,若
,若![]() 则
则![]() 或
或![]() ”是真命题
”是真命题
C.命题“若![]() 则函数
则函数![]() 只有一个零点”的逆命题为真命题
只有一个零点”的逆命题为真命题
D.“![]() 在
在![]() 上恒成立”
上恒成立”![]() 在
在![]() 上恒成立
上恒成立
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com