
【题目】已知函数f(x)=(|x|﹣b)2+c,函数g(x)=x+m.
(1)当b=2,m=﹣4时,f(x)≥g(x)恒成立,求实数c的取值范围;
(2)当c=﹣3,m=﹣2时,方程f(x)=g(x)有四个不同的解,求实数b的取值范围.
【答案】(1)c≥﹣![]() ;(2)b≥1且1<b<
;(2)b≥1且1<b<![]() .
.
【解析】
试题(1)代入b=2,m=﹣4,![]() ,去绝对值变形为c≥x﹣4﹣(|x|﹣2)2=
,去绝对值变形为c≥x﹣4﹣(|x|﹣2)2=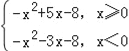 ,只需求得右边分段函数的最大值.(2)代入c=﹣3,m=﹣2
,只需求得右边分段函数的最大值.(2)代入c=﹣3,m=﹣2
,得(|x|﹣b)2=x+1有四个不同的解,所以(x﹣b)2=x+1(x≥0)有两个不同解且
(x+b)2=x+1(x<0)也有两个不同解,两个二次函数均在各自区间上有两个实数解,由根的分布,可解出b的范围.
试题解析:(1)∵当b=2,m=﹣4时,f(x)≥g(x)恒成立,
∴c≥x﹣4﹣(|x|﹣2)2=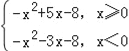 ,由二次函数的性质得c≥﹣
,由二次函数的性质得c≥﹣![]() .
.
(2)(|x|﹣b)2﹣3=x﹣2,即(|x|﹣b)2=x+1有四个不同的解,
∴(x﹣b)2=x+1(x≥0)有两个不同解以及(x+b)2=x+1(x<0)也有两个不同解,
由根的分布得b≥1且1<b<![]() ,
,
∴1<b<![]() .
.


科目:高中数学 来源: 题型:
【题目】![]() 的内切圆与三边
的内切圆与三边![]() 的切点分别为
的切点分别为![]() ,已知
,已知![]() ,内切圆圆心
,内切圆圆心![]() ,设点A的轨迹为R.
,设点A的轨迹为R.
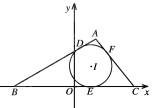
(1)求R的方程;
(2)过点C的动直线m交曲线R于不同的两点M,N,问在x轴上是否存在一定点Q(Q不与C重合),使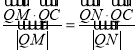 恒成立,若求出Q点的坐标,若不存在,说明理由.
恒成立,若求出Q点的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() ,其中a为常数,e是自然对数的底数,
,其中a为常数,e是自然对数的底数,![]() ,曲线
,曲线![]() 在其与y轴的交点处的切线记作
在其与y轴的交点处的切线记作![]() ,曲线
,曲线![]() 在其与x轴的交点处的切线记作
在其与x轴的交点处的切线记作![]() ,且
,且![]() .
.
(1)求![]() 之间的距离;
之间的距离;
(2)对于函数![]() 和
和![]() 的公共定义域中的任意实数
的公共定义域中的任意实数![]() ,称
,称![]() 的值为函数
的值为函数![]() 和
和![]() 在
在![]() 处的偏差.求证:函数
处的偏差.求证:函数![]() 和
和![]() 在其公共定义域内的所有偏差都大于2.
在其公共定义域内的所有偏差都大于2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中医药,是包括汉族和少数民族医药在内的我国各民族医药的统称,是反映中华民族对生命、健康和疾病的认识,具有悠久历史传统和独特理论及技术方法的医药学体系,是中华民族的瑰宝.某科研机构研究发现,某品种中医药的药物成分甲的含量![]() (单位:克)与药物功效
(单位:克)与药物功效![]() (单位:药物单位)之间具有关系
(单位:药物单位)之间具有关系![]() .检测这种药品一个批次的5个样本,得到成分甲的平均值为4克,标准差为
.检测这种药品一个批次的5个样本,得到成分甲的平均值为4克,标准差为![]() 克,则估计这批中医药的药物功效的平均值为( )
克,则估计这批中医药的药物功效的平均值为( )
A.22药物单位B.20药物单位C.12药物单位D.10药物单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业新研发了一种产品,产品的成本由原料成本及非原料成本组成.每件产品的非原料成本![]() (元)与生产该产品的数量
(元)与生产该产品的数量![]() (千件)有关,经统计得到如下数据:
(千件)有关,经统计得到如下数据:
![]()
根据以上数据,绘制了散点图.
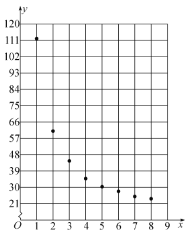
观察散点图,两个变量不具有线性相关关系,现考虑用反比例函数模型![]() 和指数函数模型
和指数函数模型![]() 分别对两个变量的关系进行拟合.已求得用指数函数模型拟合的回归方程为
分别对两个变量的关系进行拟合.已求得用指数函数模型拟合的回归方程为![]() ,
,![]() 与
与![]() 的相关系数
的相关系数![]() .参考数据(其中
.参考数据(其中![]() ):
):

(1)用反比例函数模型求![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)用相关系数判断上述两个模型哪一个拟合效果更好(精确到0.01),并用其估计产量为10千件时每件产品的非原料成本;
(3)该企业采取订单生产模式(根据订单数量进行生产,即产品全部售出).根据市场调研数据,若该产品单价定为100元,则签订9千件订单的概率为0.8,签订10千件订单的概率为0.2;若单价定为90元,则签订10千件订单的概率为0.3,签订11千件订单的概率为0.7.已知每件产品的原料成本为10元,根据(2)的结果,企业要想获得更高利润,产品单价应选择100元还是90元,请说明理由.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: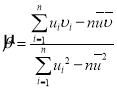 ,
,![]() ,相关系数
,相关系数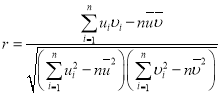 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面为正方形,△PAD为等边三角形,平面PAD丄平面PCD.
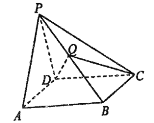
(1)证明:平面PAD丄平面ABCD:
(2)若AB=2,Q为线段的中点,求三棱锥Q-PCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在六棱锥P﹣ABCDEF中,六边形ABCDEF为正六边形,平面PAB⊥平面ABCDEF,AB=1,PA![]() ,PB=2.
,PB=2.
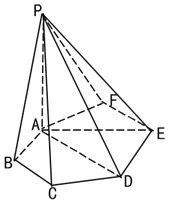
(1)求证:PA⊥平面ABCDEF;
(2)求直线PD与平面PAE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD-A1B1C1D1的底面为菱形,AA1⊥底面ABCD,∠BAD=120°,AB=2,E,F分别为CD,AA1的中点.
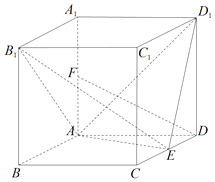
(Ⅰ)求证:DF∥平面B1AE;
(Ⅱ)若直线AD1与平面B1AE所成角的正弦值为![]() ,求AA1的长;
,求AA1的长;
(Ⅲ)在(Ⅱ)的条件下,求二面角B1-AE-D1的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com