【题目】若圆
上至少有三个不同的点到直线
的距离为
，则直线l的倾斜角的取值范围是（ ）
A.
B.
C.
D.
【答案】D
【解析】
把圆的方程化为标准方程，找出圆心A的坐标和半径r的值，由圆A上有且仅有三个不同点到直线l的距离为
，则圆心A到直线l的距离等于r
，故利用点到直线的距离公式列出关于k的方程，求出方程的解得到k的取值范围，然后根据直线斜率与倾斜角的关系，利用两角和与差的正切函数公式及特殊角的三角函数值即可求出直线l的倾斜角．
由圆
的标准方程（x﹣2）2+（y﹣2）2＝18，则圆心为（2，2），半径为
，设直线
为y＝kx
圆上至少有三个不同的点到直线的距离为，则圆心到直线的距离应不大于等于r=
，
∴
整理得：k2﹣4k+1≤0，解得：2
k≤2
，
由tan15°＝tan（45°﹣30°）
2
，
tan75°＝tan（45°+30°）
2，
k＝tanα，则直线l的倾斜角的取值范围
，
故选：D．
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案科目：高中数学 来源： 题型：
【题目】定义在
上的函数
，若满足:对任意
，存在常数
，都有
成立，则称是上的有界函数，其中
称为函数的上界
（1）设
，判断在
上是否是有界函数，若是，说明理由，并写出所有上界的值的集合；若不是，也请说明理由.
（2）若函数
在
上是以
为上界的有界函数，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列说法中，正确的是（ ）
A. 命题“若
，则
”的逆命题是真命题
B. 命题“存在
”的否定是：“任意
”
C. 命题“p或q”为真命题，则命题“p”和命题“q”均为真命题
D. 已知
，则“
”是“
”的充分不必要条件
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，在四棱锥P-ABCD中，AB⊥平面PAD，AB∥CD，PD=AD，E是PB的中点，F是DC上的点且DF=
AB，PH为△PAD边上的高.
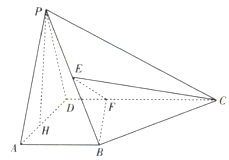
（1）证明：PH⊥平面ABCD；
（2）若PH=1，AD=
，FC=1，求三棱锥E-BCF的体积；
（3）证明：EF⊥平面PAB.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在四棱锥V-ABCD中，底面ABCD是正方形，侧面VAD是正三角形，平面VAD⊥底面ABCD．
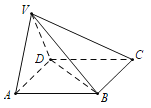
（Ⅰ）证明AB⊥平面VAD；
（Ⅱ）求面VAD与面VDB所成二面角的大小．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，正方体
的棱长为a，
分别是棱
、
的中点，过点的平面分别与棱
、
交于点
，设
，
，给出以下四个命题：
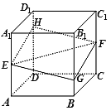
（1）平面
与平面
所成角的最大值为
；
（2）四边形的面积的最小值为
；
（3）四棱锥
的体积为
；
（4）点
到平面的距离的最大值为
，
其中正确的个数为（ ）
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
